The Binomial Expansion

This tutorial is developed in such a way that even a student with modest mathematics background can understand this particular topics in mathematics. It normally comes in core mathematics module 2 at AS Level.

Throughout the tutorial - and beyond it - students are discouraged from using the calculator in order to find nCr values. Instead, the use of Pascal's Triangle is encouraged, which is much faster than pressing down a series of calculator buttons.

Factorial - n!

The factorial of a number is defined as follows:

n! = n(n-1)n-2)(n-3).......1

E.g.

3! = 3 X 2 X 1 = 6

4! = 4 X 3 X 2 X 1 = 24

5! = 5 X 4 X 3 X 2 X 1 = 120

The factorial of both 0 and 1 are defined as 1 - 0! = 1; 1! = 1.

Factorial Calculator - n!

n  

Now, let's deal with some simple calculations involving the factorials of numbers:

E.g.1

Find 5!/3!

5!/3! = 5 X 4 X 3!/3!
= 5 X 4
= 20
We stop the expansion of the top factorial at 3 so that the factorial of 3 at the bottom can be cancelled out.

E.g.2

Find 6!/4!

6!/4! = 6 X 5 X 4!/4!
= 6 X 5
= 30
We stop the expansion of the top factorial at 4 so that the factorial of 4 at the bottom can be cancelled out.

E.g.3

Find 6!/5!

6!/5! = 6 X 5!/5!
= 6
= 6
We stop the expansion of the top factorial at 5 so that the factorial of 5 at the bottom can be cancelled out.

E.g.4

Find 6!/(4! 2!)

6!/(4! 2!) = 6 X 5 X 4!/(4! 2!)
= 6 X 5 X 4!/ 4! 2!
= 30 / 2!
= 30/2
= 15 We stop the expansion of the top factorial at 4, the bigger factorial of the denominator, so that the factorial of 4 at the bottom can be cancelled out.

E.g.5

Find 6!/(5! 1!)

6!/(5! 1!) = 6 X 5!/(5! 1!)
= 6 X 5!/ 5! 1!
= 6 / 1!
= 6 / 1
= 6 We stop the expansion of the top factorial at 5, the bigger factorial of the denominator, so that the factorial of 5 at the bottom can be cancelled out.

E.g.6

Find 6!/(6! 0!)

6!/(6! 0!) = 6!/(6! 0!)
= 6!/ 6! 0!
= 1 / 0!
= 1 / 1
= 1 We stop the expansion of the top factorial at 6, the bigger factorial of the denominator, so that the factorial of 6 at the bottom can be cancelled out.

Combinations - nCr

nCr = n!/(n-r)!r!

E.g.1

Find 6C2.

6C2 = 6!/(6-2)!2!
= 6! / 4! 2!
= 6 X 5 X 4!/4! 2!
= 30 / 2!
= 30 / 2
= 15

E.g.2

Find 6C2.

7C5 = 7!/(7-5)!5!
= 7! / 2! 5!
= 7 X 6 X 5!/2! 5!
= 42 / 2!
= 30 / 2
= 21

E.g.3

Find 8C1.

8C1 = 8!/(8-1)!1!
= 8! / 7! 1!
= 8 X 7!/7! 1!
= 8 / 1!
= 8 / 1
= 8

E.g.4

Find 8C0.

8C0 = 8!/(8-0)!0!
= 8! / 8! 0!
= 8!/8! 0!
= 1 / 0!
= 1 / 1
= 1

Pascal's Triangle

Pascal's triangle gives all the nCr values of the n^th row of the triangle.

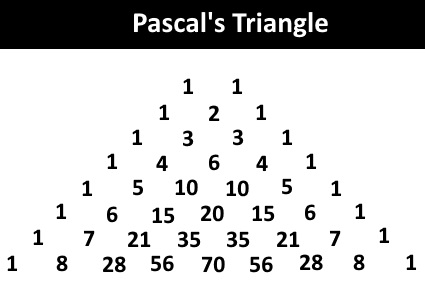
E.g.

For example, take the 6^th row:
6C0 = 1
6C1 = 6
6C2 = 15
6C3 = 20
6C4 = 15
6C5 = 6
6C6 = 1

Now you can experiment with it using the calculator given below:

Calculator for finding nCr

n:    r:  

 

Formula for Binomial Expansion

(1 + x)ⁿ =Σ nCr x^r

It is easier to get nCr values from Pascal's Triangle than from a calculator; typing takes time!

E.g.1

Expand (1 + x)⁵

(1 + x)⁵ = Σ 5Cr x^r
= 5C0 x⁰ + 5C1 x¹ + 5C2 x² + 5C3 x³ + 5C4 x⁴ + 5C5 x⁵
= 1 + 5x + 10x² + 10x³ + 5x⁴ + x⁵

E.g.2

Expand (1 + x)³

(1 + x)³ = Σ 3Cr x^r
= 3C0 x⁰ + 3C1 x¹ + 3C2 x² + 3C3 x³
= 1 + 3x + 3x² + x³

E.g.3

Expand (1 + 2x)⁵

(1 + 2x)⁵ = Σ 5Cr (2x)^r
= 5C0 (2x)⁰ + 5C1 (2x)¹ + 5C2 (2x)² + 5C3 (2x)³ + 5C4 (2x)⁴ + 5C5 (2x)⁵
= 1 + 10x + 40x² + 80x³ + 80x⁴ + 32x⁵

E.g.4

Expand (1 + x/2)⁵

(1 + x/2)⁵ = Σ 5Cr (x/2)^r
= 5C0 (x/2)⁰ + 5C1 (x/2)¹ + 5C2 (x/2)² + 5C3 (x/2)³ + 5C4 (x/2)⁴ + 5C5 (x/2)⁵
= 1 + 5/2x + 5/2x² + 5/4x³ + 5/16x⁴ + x⁵/32

E.g.5

Expand (1 - x)⁵

(1 + (-x))⁵ = Σ 5Cr (-x)^r
= 5C0 (-x)⁰ + 5C1 (-x)¹ + 5C2 (-x)² + 5C3 (-x)³ + 5C4 (-x)⁴ + 5C5 (-x)⁵
= 1 - 5x + 10x² - 10x³ + 5x⁴ - x⁵

E.g.6

Expand (2 + x)⁵

Take 2 out in order to perform binomial expansion
[2(1 + x/2)]⁵ =2⁵[ Σ 5Cr (x/2) ]^r
= 2⁵[5C0 (x/2)⁰ + 5C1 (x/2)¹ + 5C2 (x/2)² + 5C3 (x/2)³ + 5C4 (x/2)⁴ + 5C5 (x/2)⁵]
= 2⁵[1 + 5/2 x + 5/2 x² + 5/4 x³ + 5/16 x⁴ + x⁵/32]
= 32 + 80x + 80x² + 40x³ + 10x⁴ + x⁵

E.g.7

Find the coefficient of the third term of (3 + 2x)⁵

[3(1 + 2x/3)]⁵ =3⁵[ Σ 5Cr (2x/3) ]^r
The third term is 3⁵ X 5C2 X (2x/3)²
3⁵ X 10 X 4x²/3²
3³ X 10 X 4x²
1080x²
So, the coefficient of the 3^rd term is 1080.

E.g.8

Show that nCr = nC(n-r)
nCr = n!/(n-r)! r! = n(n-1)(n-2)...(n-r+1)(n-r)!/(n-r)! r! = n(n-1)(n-2)...(n-r+1)/r!
nC(n-r)! = n!/(n-r)! r! = n(n-1)(n-2)...(n-r+1)(n-r)!/(n-(n-r))!(n-r)! = n(n-1)(n-2)...(n-r+1)(n-r)!/r!(n-r)!= n(n-1)(n-2)...(n-r+1)/r!
nCr = nC(n-r)

The Binomial Expansion - negative indices and fractions

(1 + x)ⁿ = Σ nCr
nC0 x⁰ + nC1 x + nC2 x² + nC3 x³ + ......+ nCn xⁿ
1 + nx + n(n-1)!/2!(n-2)! x² + n(n-1)(n-2)(n-3)!/3! x³ +.......
1 + nx + n(n-1)/2 x² + n(n-1)(n-2)/6 x³ +......
if x is very small - |x|<1 or -1< x <1 - the higher powers of x are getting too small and become insignificant.
So, the expansion can be stopped as follows:

(1 + x)ⁿ ≈ 1 + nx + n(n-1)/2 x² + n(n-1)(n-2)/6 x³

Note the almost equal sign, instead of the equal sign.

E.g.1

Expand (1 + x)^1/2 up to the fourth term.
(1 + x)ⁿ ≈ 1 + nx + n(n-1)/2 x² + n(n-1)(n-2)/6 x³
(1 + x)^1/2 ≈ 1 + (1/2)x + (1/2)(-1/2)/2 x² + (1/2)(-1/2)(1/2-2)/6 x³
(1 + x)^1/2 ≈ 1 + (1/2)x - (1/4)/2 x² + (3/16)/6 x³
(1 + x)^1/2 ≈ 1 + (1/2)x - (1/8) x² - (1/16) x³

E.g.2

(1 + x)ⁿ ≈ 1 + nx + n(n-1)/2 x² + n(n-1)(n-2)/6 x³
(1+x)⁻³ ≈ 1+(−3) x + (−3)(−4)/2! + x² + (−3)(−4)(−5)/3! x³
(1+x)⁻³ ≈ 1 −3x + 6x² − 10x³

E.g.3

Expand (1 + 2x)^-3 and state the value/s of x for which the expansion is valid.
(1 + x)ⁿ ≈ 1 + nx + n(n-1)/2 x² + n(n-1)(n-2)/6 x³
(1 + 2x)^-3 ≈ 1 + (−3)(2x) + (−3)(−4)(2x )²/2! +(−3)(−4)(−5)(2x)³/3!
≈ 1 − 6x + 24x² − 80x³
The expansion is valid if |2x| < 1
|x| <1/2 or -1/2 < x < 1/2

E.g.4

Expand (1 - x)^-5 and state the value/s of x for which the expansion is valid.
(1 - x)ⁿ ≈ 1 + nx + n(n-1)/2 x² + n(n-1)(n-2)/6 x³
(1 - x)^-5 ≈ 1 + (−5)(-x) + (−5)(−6)(-x )²/2! +(−5)(−6)(−7)(-x)³/3!
≈ 1 + 5x + 15x² + 35x³
The expansion is valid if |-x| < 1
|x| < 1 or -1 < x < 1

E.g.5

Expand (1 + 3x)^1/2 and hence find an approximation for √103.
(1 + x)ⁿ ≈ 1 + nx + n(n-1)/2 x² + n(n-1)(n-2)/6 x³
(1 + 3x)^1/2 ≈ 1 + (1/2)(3x) + (1/2)(1/2-1)(3x)²/2! +(1/2)(1/2-1)(1/2-2)(3x)³/3!
≈ 1 + (3/2)x + (-9/8)x² − (27/16)x³
Let x = 0.01
Then, (1 + 3 X 0.01)^1/2 ≈ 1 + (3/2)0.01 + (-9/8)0.01² − (27/16)0.01³
(1 + 3 X 0.01)^1/2 ≈ 1 + (0.03/2) + (-0.0009/8) − (0.000027/16)
(1 + .03)^1/2 ≈ 1 + 0.015 -0.0001125 − 0.0000017
(1 + 0.03)^1/2 ≈ 1.0148858
(1 + 3/100)^1/2 ≈ 1.0148858
(103/100)^1/2 ≈ 1.0148858
103^1/2/10 ≈ 1.0148858
√103 ≈ 10.148858
√103 ≈ 10.149(3 d.p)

Do you need the tutorial with more worked examples as a Kindle Book? Here is the link for Amazon: