Integration - The Trapezium Rule / Trapezoidal Rule or Trapezoid Rule

The area between a function and the x-axis can be calculated by integration provided that the function in question can be integrated by known techniques. Sometimes we come across functions which cannot be integrated, though. In such situations, we use the Trapezium Rule to deal with it. The Trapezium Rule never gives the exact area, but an approximate value of the area.

The technique involves the division of the area into a finite number of steps of equal width. If the width is narrow enough, each strip can be treated as a trapezium.

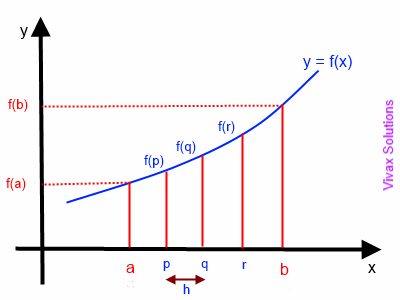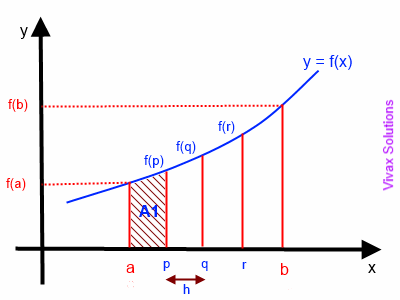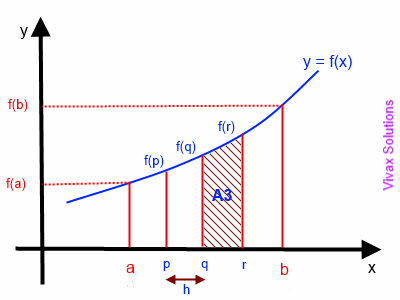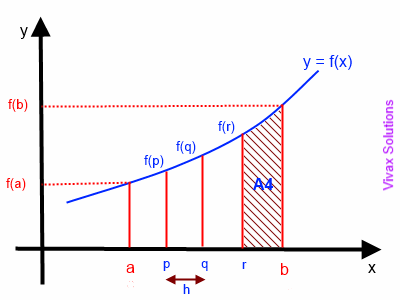
Suppose the area under the curve is divided into four strips of equal width h; the shape of each strip is nearly a trapezium. So, let's calculate the area of each trapezium.

A1 = h/2 [f(a) + f(p)]
A2 = h/2 [f(p) + f(q)]
A3 = h/2 [f(q) + f(r)]
A4 = h/2 [f(r) + f(b)]

So, Total Area = h/2 [ f(a) + 2f(p) + 2f(q) + 2f(r) + f(b)]

If there are n number of strips of width h, the formula simply takes the following form:

Area = h/2 [ f(a) + 2f(1) + 2f(2) + 2f(3) + 2f(4) + ...... + 2f(n - 1) + f(b) ]

h = (b - a)/n

In order to maximize the accuracy, the number of strips must be increased. It can, however, make the calculations a bit more cumbersome.

 

E.g.1

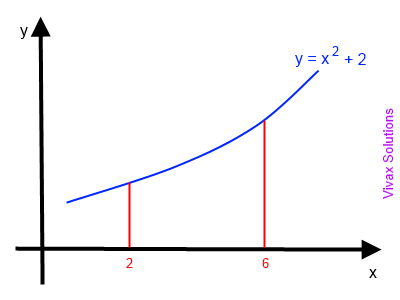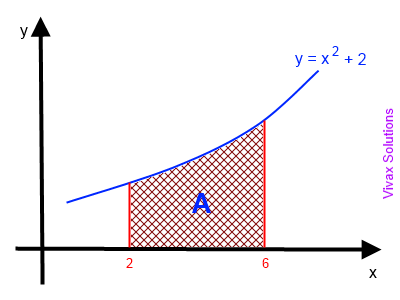
Find the area under the curve, y = x² + 2, between x = 2 and x = 6.

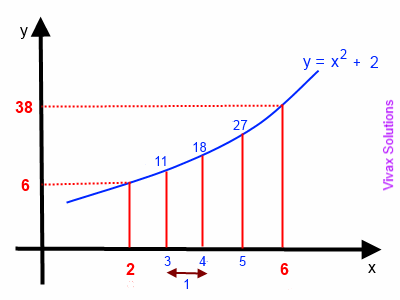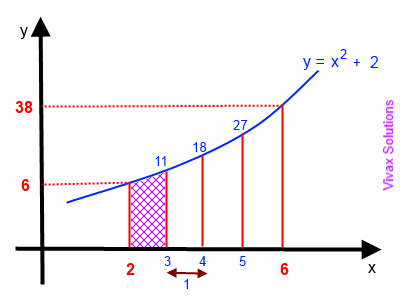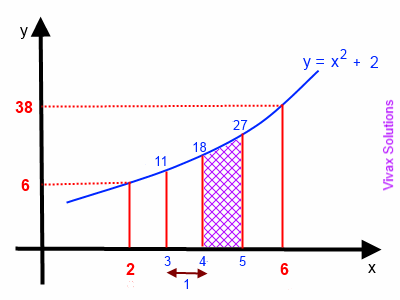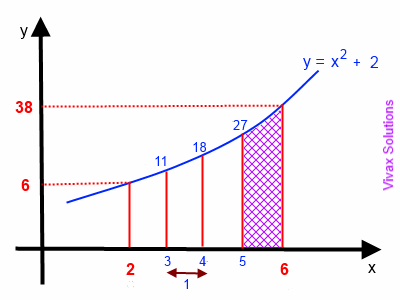
Let's divide the area into four equal strips and do the calculations first.
So, h = (6 -2)/4 = 1
A = 1/2[ f(2) + 2f(3) + 2f(4) + 2f(5) + f(6)]
= 1/2[6 + 2(11) + 2(18) + 2(27) + 38]
= 1/2[6 + 22 + 36 + 54 + 38]
= 1/2[156] = 78

Now, let's use integration to find the exact area under the curve between x = 2 and x = 6.

A = ₂∫⁶ (x² + 2)dx
= [ x³/3 + 2x]₂⁶
= [216/3 + 2X6] - [8/3 + 2X2]
= 77.3

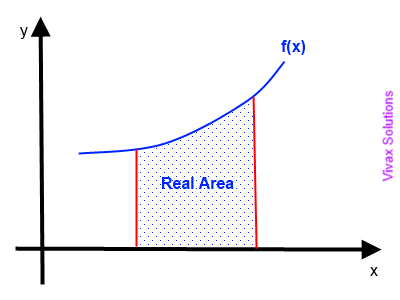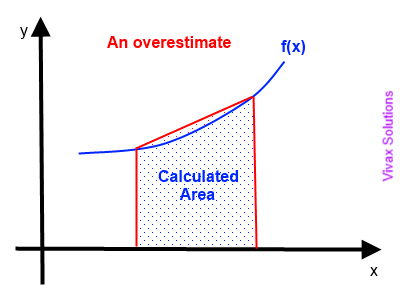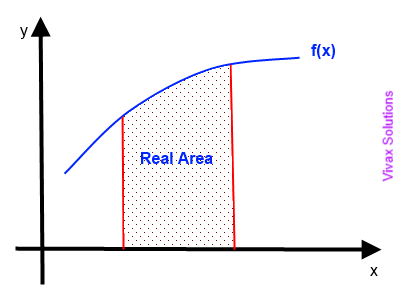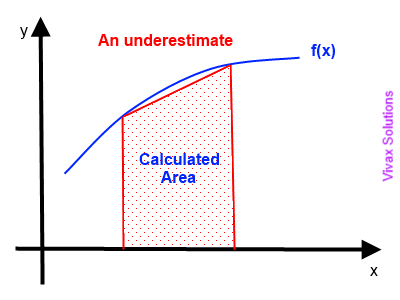
The value of the real area is significantly lower than that we got from the trapezium rule. This is because the strips that we use are not thin enough for a greater accuracy. In short, it was an over estimate.

E.g.2

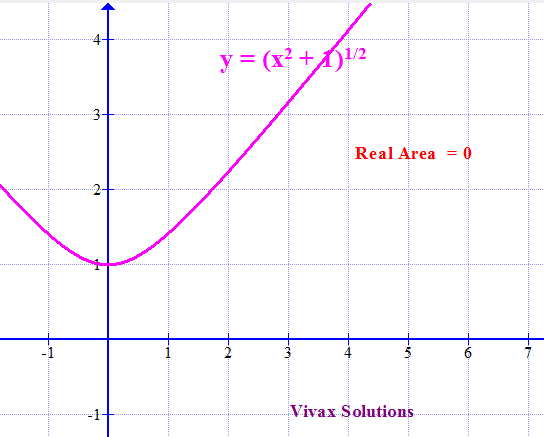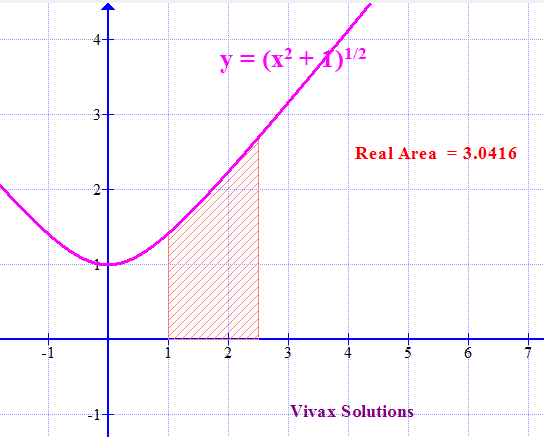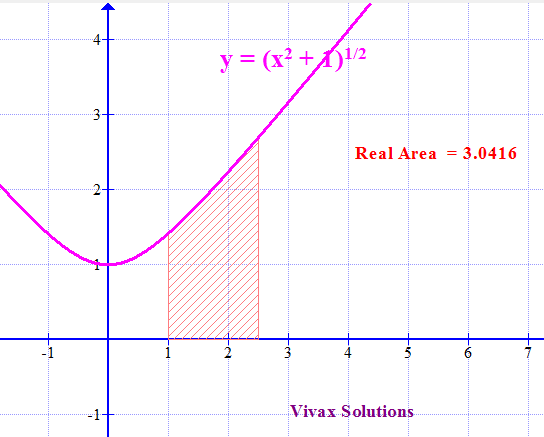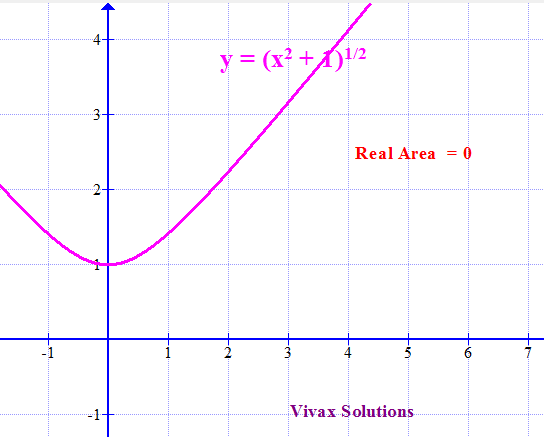
Calculate the area between x=1 and x= 3 of the curve, y = √x²+1 and the x-axis.

Let's use the following formula to work out the area:

So, Total Area = h/2 [ f(a) + 2f(p) + 2f(q) + 2f(r) + f(b)]

 

 

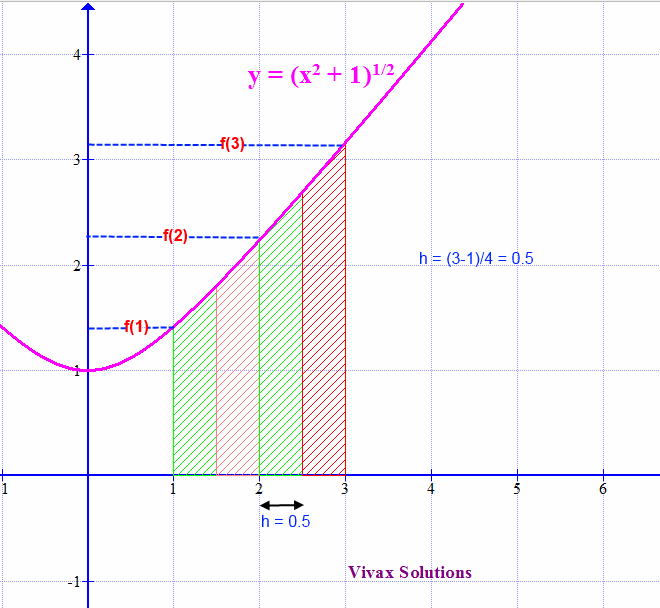
In this case, let's use four strips. Therefore, the width of each strip, h, is 0.5. The following table summarizes the f(x) values:

x	1	1.5	2.0	2.5	3.0
y	1.41	1.58	2.34	2.69	3.16

So, the total area of the strips = (0.5/2)[ 1.41 + 2 X 1.58 + 2 X 2.34 + 2 X 2.69 + 3.16 ] = 4.4475

The following animation shows the real area under the curve:

 

 

Trapezium Rule - interactive

In the following applet, you can change the number of stripes, n, and see how it affects the area under the curve; the more stripes there are, the greater the accuracy.

Error in the Calculation of Areas

As you can see, the area from the Trapezium Rule is slightly less than the real value, given by integration as shown in the animation.

It is important to be aware of the inevitable errors when we use the Trapezium Rule. The following animation clearly shows it.