Bearings Tutorial

Since we are fairly familiar with the four main directions - North, South, East and West - there is not going to be an issue in identifying them, as long as we know where North is.

The problem, however, arises when we have to express the direction between any two of them - and as a numerical value for accuracy.

By expressing the direction in terms of bearings we can overcome a catalogue of practical difficulties in the field of navigation.

Bearings in Practice

Just look at the sky in the following animation near Heathrow, in the United Kingdom; how do aircraft controllers stop these planes from collisions in a saturated sky? It is the role of three-figure-bearings that help keep the order in our skies.

 

 

This tutorial helps you understand the concept effectively using an interactive programme.

 

Bearings

A bearing is defined as an angle measured clockwise from the north direction.

A bearing is usually expressed in three numbers; therefore, it is called 3-number-bearing.

E.g.

30⁰ is expressed as 030⁰.

130⁰ is expressed as 130⁰.

330⁰ is expressed as 330⁰.

Click the mouse along the slider and watch the updating below for the bearing.

 

E.g.1

The bearing of B from A is 020⁰. Find the bearing of A from B.

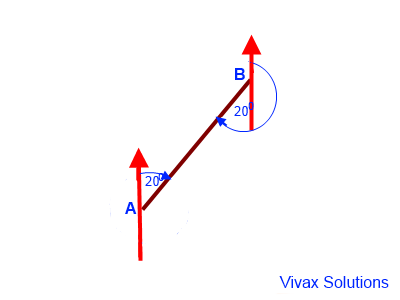
The bearing of A from B = 180 + 20 = 200⁰.

E.g.2

The bearing of B from A is 120⁰. Find the bearing of A from B.

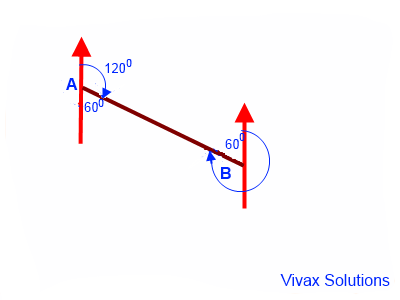
The bearing of A from B = 360 - 60 = 300⁰.

E.g.3

The bearing of B from A is 220⁰. Find the bearing of A from B.

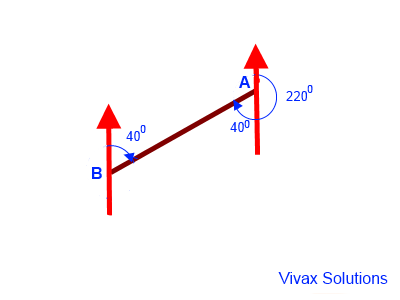
The bearing of A from B = 040⁰.

E.g.4

The bearing of B from A is 310⁰. Find the bearing of A from B.

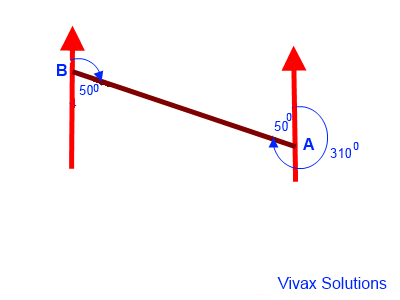
The bearing of A from B = 180 - 50 = 130⁰.

E.g.5

The following is a map of a part of the United Kingdom. Calculate the bearings of the following cities:

1. Bristol from Birmingham
2. Birmingham from London
3. London from Bristol

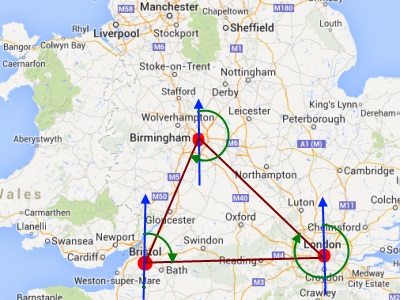
1. The bearing of Bristol from Birmingham = 180 + 22 = 202⁰.
2. The bearing of Birmingham from London = 360 -45 = 315⁰.
3. The bearing of London from Bristol = 087⁰.

 

Amazon Best Sellers:

These flash cards will make a significant difference when you revise for your forthcoming exams: very informative and neatly presented; they became best sellers for a reason.

 

Practice 1:

By using a protractor on the screen, find the following bearings:

1. Birmingham from Bristol
2. Bristol from London
3. London from Birmingham

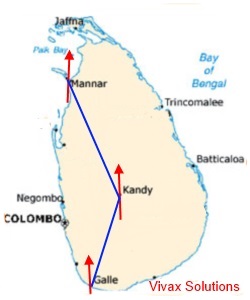
Practice 2:

By using a protractor on the screen, find the following bearings:

1. Mannar from Kandy
2. Kandy from Galle
3. Mannar from Galle