Odd and Even functions

Advanced maths - odd and even functions tutorial

Even Functions

If a function exists such that f(x) = f(-x), it is called an even function.

E.g.

 

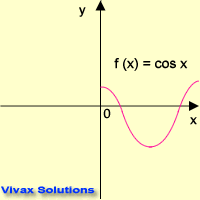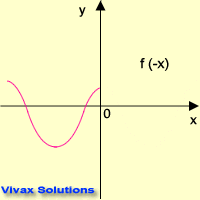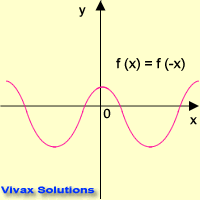
f(x) = cos x
This animation shows f(x) = f(-x).
Therefore, f(x) = cos x is an even function.

E.g.

Show that f(x) = 2x⁴ + x² is an even function.

f(x) = 2x⁴ + x²
f(-x) = 2(-x)⁴ + (-x)²
f(-x) = 2x⁴ + x² = f(x)

Therefore, f(x) = 2x⁴ + x² is an even function.

Odd Functions

If a function exists such that f(x) = -f(-x), it is called an odd function.

E.g.

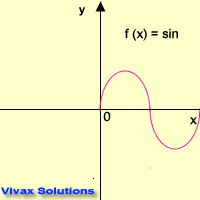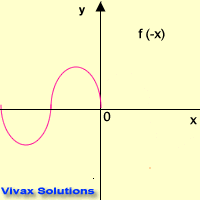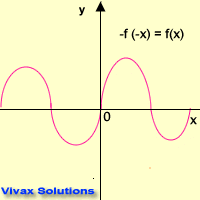
f(x) =sin x
This animation shows f(x) = -f(-x).
Therefore, f(x) = sin x is an even function.

E.g.

Show that f(x) = x³ + 2x is an odd function.
f(x) = x³ + 2x
f(-x) = (-x)³ + 2(-x) = -x³ -2x
-f(-x) = x³ + 2x = f(x)

Therefore, f(x) = x³ + 2x is an odd function.

Practice is the key to mastering maths; please visit this page, for more worksheets.

Please work out the following questions to complement what you have just learnt.

1. Show by drawing or otherwise that f(x) = 1/x and f(x) = x³ are odd functions.
2. Show that f(x) = (x - 2)(x + 2)/(x² + 2) is an even function.
3. Check whether f(x) = x³ / (x² + 7) is odd or even.
4. Show that f(x) = (x³ + x) /(x³ - x) is an even function.