Hyperbolic Functions

Functions that are defined in terms of the exponential function or its derivatives are called hyperbolic functions.

 

The exponential function and its derivatives take these forms.

E.g

sinh x = (e^x - e^-x) / 2

cosh x = (e^x + e^-x) / 2

tanh x = sinh x / cosh x = (e^x - e^-x) / (e^x + e^-x)

In order to obtain the values of hyperbolic functions, the following table can be used.

Enter 'x' here

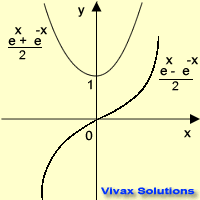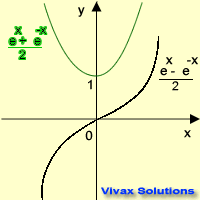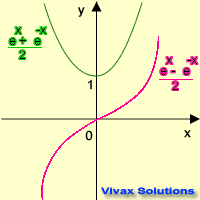
Let's see the graphical representation of the three hyperbolic functions.

 

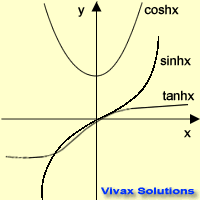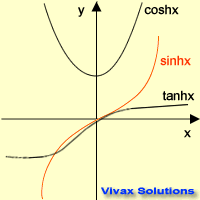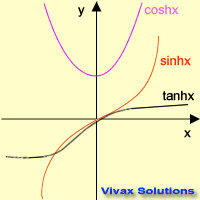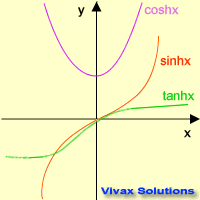
Now, the basic properties of these functions can easily be derived:

E.g.1

cosh-x = cosh x
cosh x = (e^x + e^-x) / 2
cosh -x = (e^(-x) + e^-(-x)) / 2 = (e^x + e^-x) / 2 = cosh x

E.g.2

sinh -x = -sinh x
sinh x = (e^x - e^-x) / 2
sinh -x = (e^(-x) - e^-(-x)) / 2 = (e^-x - e^x) / 2 = - sinh x

E.g.3

tanh -x = -tanh x
tanh x = (e^x - e^-x) / (e^x + e^-x)
tanh -x = (e^-x - e^-(-x)) / (e^-x + e^-(-x)) = (e^-x - e^x) / (e^-x + e^x) = -tanh x

The functions can be extended to bring about the following identities.

1. cosh(a + b) = cosh(a)cosh(b) + sinh(a)sinh(b)
2. sinh(a + b) = sinh(a)cosh(b) + cosh(a)sinh(b)
3. cosh(a - b) = cosh(a)cosh(b) - sinh(a)sinh(b)
4. sinh(a - b) = sinh(a)cosh(b) - cosh(a)sinh(b)
5. tanh (a+b) = tanh a + tanh b /(1 + tanh a.tanh b)

Please work out the following questions to complement what you have just learnt.

1. Show that tanh x is an odd function.
2. Show that cosh²x - sinh²x = 1
3. Differentiate y = sinh x and y = cosh x
4. Prove that cosh x is even and sinh x is odd.
5. Find the point on y = cosh x curve, where the gradient is one.