Differential Equations

An equation in the form of dy/dx = f(x) g(y) is called a differential equation of the first order, where f(x) and g(y) are functions of x and y respectively

E.g.

dy/dx = xy is a differential equation where x and y are functions of x and y respectively.

In order to integrate a differential equation, the variables must be separated as follows:

dy/dx = f(x) g(y)
dy/g(y) = f(x) dx

E.g.1

dy/dx = xy
∫ dy/y = ∫ x dx
ln y = x²/2 + c
y = e^{x2 + c}

E.g.2

dy/dx = cos²y e^x
dy/cos²y = e^x dx
∫ dy/cos²y = ∫ e^x dx
∫ dy sec²y = ∫ e^x dx
tan y = e^x + c

Exponential Growth / Decay

If a rate of change is proportional to its quantity, such a rate is called Exponential Growth / Decay.

E.g.1

The rate of increase in population of a colony of bacteria is proportional to the number of bacteria in the colony at a given time. Therefore, such a rate of increase is an exponential growth.

So, dN/dt ∝ N
dN/dt = k N
dN/N = k dt
∫ dN/N = ∫ k dt
ln N = kt + c
N = e^kt + c
N = e^kt X e^c ---- 1
Let N = N₀ when t = 0
N₀ = e^c
Sub this in 1
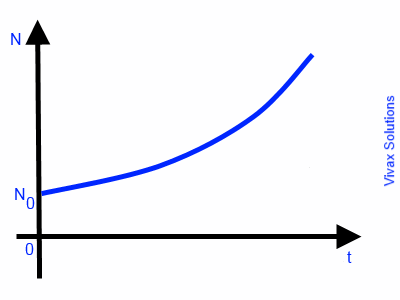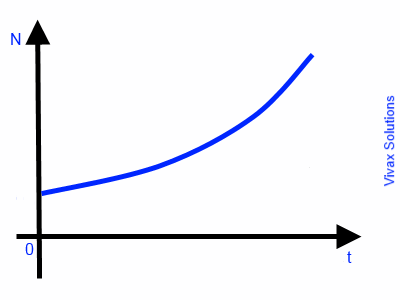
N = N₀e^kt
This is exponential growth. The following image indicates the graphical nature of the growth.

E.g.2

The rate of decay of radioactive nuclei in a radioactive substance is directly proportional to the number of remaining nuclei at a given time. Therefore, this is an exponential decay.

So, dN/dt ∝ -N ---- the negative sign indicates a decay or a loss
dN/dt = -k N
dN/N = -k dt
∫ dN/N = ∫ k dt
ln N = -kt + c
N = e^-kt + c
N = e^-kt X e^c ---- 1
Let N = N₀ when t = 0
N₀ = e^c
Sub this in 1
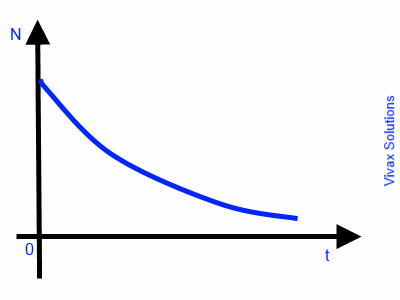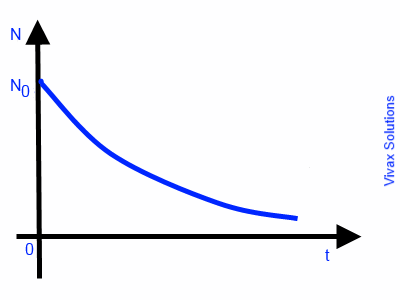
N = N₀e^-kt
This is exponential decay. The following image indicates the graphical nature of the decay against time.