A Tutorial on Pulleys

A pulley is a mechanical device over which a string can be moved to facilitate the movement of the objects attached to it. It is a wheel on an axle. It support the motion of the objects or cables that run over its circumference.

Pulleys have been in use since time immemorial. The ancient Egyptians, for instance, used them extensively in transporting huge boulders to pyramid building sites from distant quarries.

It is important to understand how pulley mechanics work, before mastering their uses - exactly as our forefathers did.

Let's consider two objects, connected by a string and then placed over a smooth pulley. Depending on the nature of the masses of the objects, the string will move the objects clockwise or anticlockwise. In this tutorial we assume the string is inextensible and light - tension of the string remains the same at any point - and the pulley is smooth - no room for friction.

Case 1

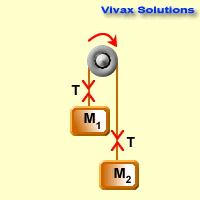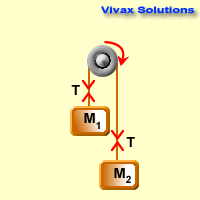
Since M₂ > M₁,
F = ma for the heavier object,
M₂g - T = M₂a 1
F = ma for the lighter object,
T - M₁g = M₁a 2
1 + 2 =>M₂g - M₁g = (M₁ + M₂)a
a = (M₂g - M₁g)/ (M₁ + M₂)

Case 2

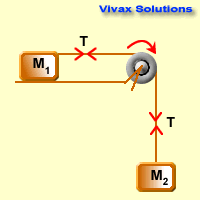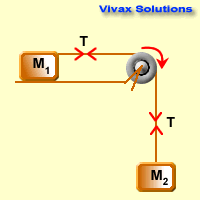
Since M₂ > M₁,
F = ma for the heavier object,
M₂g - T = M₂a 1
F = ma for the lighter object,
T = M₁a 2 (assumed the table to be smooth - no friction)
1 + 2 =>M₂g = (M₁ + M₁)a
a = M₂g / (M₁ + M₂)

Case 3

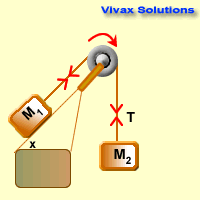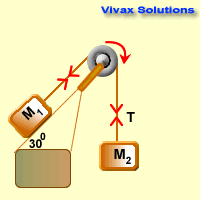
Since M₂ > M₁,
F = ma for the heavier object,
M₂g - T = M₂a 1
F = ma for the lighter object,
T - M₁g sin x = M₁a 2 (assumed the table to be smooth - no friction)
>1 + 2 =>M₂g - M₁g sin x = (M₁ + M₁)a
a = (M₂g - M₁g sin x) / (M₁ + M₂)

To make calculations easier, g is assumed as 10ms^-2 in the following examples:

E.g.1

Two masses of 6 kg and 2 kg are connected by a light inextensible string and placed over a smooth pulley. Find the acceleration of the system and tension of the string.
For the heavier object, using F = ma,
6g - T = 6a 1
For the lighter object, using F = ma,
T - 2g = 2a 2
1 + 2 => 4g = 8a
a = 5ms^-2
Sub in 1 => 6g - T = 6 x 2
60 - T = 30
T = 30 N.

E.g.2

Two masses of 8 kg and 2 kg are connected to a string and put over a smooth pulley. The system is released from rest. Find the acceleration, and the distance travelled in 4 seconds. What is the speed of the system after this period?
For the heavier object, using F = ma,
8g - T = 8a 1
For the lighter object, using F = ma,
T - 2g = 2a 2
1 + 2 => 6g = 10a
a = 6ms^-2
For the system,
u = 0, a = 6, t = 4
s = 0 x 4 + 1/2 x 6 x 16
s = 48 m
v = 0 + 6 x 4
v = 24 ms^-1

E.g.3

Two masses of 6 kg and 2 kg are connected by a light inextensible string and placed over a smooth pulley. Find the acceleration of the system and the speed after 4 seconds. Then the string is cut; how far will the lighter object move up? Calculate the time taken for that too. Calculate the distance travelled by the heavier object during the same time and the speed reached.
For the heavier object, using F = ma,
6g - T = 6a 1
For the lighter object, using F = ma,
T - 2g = 2a 2
1 + 2 => 4g = 8a
a = 5ms^-2
v = 0 + 5 x 4
v = 20 ms^-1
After the string is cut, the tension is no longer at work; so, the objects move just under gravity.
For the lighter one,
u = 20, a = -10, v = 0
v = 20 - 10 x t
10t = 20
t = 2 s.
s = 20 x 2 - 1/2 x 10 x 4
s = 40 - 20
s = 20 m.
For the heavier one,
u = 20, a = 10, t = 2
v = 20 + 10 x 2
v = 20 + 20
v = 40 ms^-1 s = 20 x 2 + 1/2 x 10 x 4
s = 60m.

E.g.4

A mass of 4 kg is placed on a smooth table and connected to string that goes over a smooth pulley at the edge of the table. The other end of the string is connected to a 6kg object. The system is released from rest. Find the acceleration of the system and the tension of the string.
For the heavier object, using F = ma,
6g - T = 6a1
For the lighter object, using F =ma,
T = 4a2
1 + 2 => 6g = 10a
a = 6ms^-2
2=> T = 4 x 6 = 24
T = 24 N.

E.g.5

A pulley is connected to the edge of a smooth plane that is at 30⁰ to the horizontal. A string goes over the pulley and its vertical part is connected to a mass of 6 kg. The other end is connected to a mass of 4 kg that is placed on the plane. The system is released from rest. Find its speed after 5 seconds and the distance travelled up the plane.
For the lighter one, using F = ma,
T - 4g sin 30 = 4a T - 20 = 4a1
For the heavier one, using F = ma
6g - T = 6a
60 - T = 6a2
1 + 2 => 40 = 10a
a = 4ms^-2
1=> T - 20 = 6 X 4 = 24
T = 24 N.

 

Challenge - 🔗

A chain of mass m and length l lies on a rough table of coefficient friction, μ, in such a way that a part of it hangs over the edge. Find the ratio of two parts, the horizontal and vertical parts, when it is about to move.

 

Practice is the key to mastering maths; please visit this page, for more worksheets.

Please work out the following questions to complement what you have just learnt.

1. Two objects of mass 8 kg and 4 kg are connected to a string that goes over a smooth pulley. The system is released from rest. Find the acceleration and the tension of the string.
2. Two objects of mass 6 kg and 4 kg are connected to a string that goes over a smooth pulley. The system is released from rest. Find the acceleration of the system. If the system is released from rest, find the speed after 10 seconds. At this moment, the heavier one hits the floor. Describe the subsequent motion of the objects afterwards, until the lighter one stops.
3. Two objects of mass 5 kg each is connected to a string that goes over a smooth pulley. A part of one object is added to the other so that the system gets a speed of 10 ms^-1 in 5 seconds. Find the mass removed from one object.
4. A mass of 4 kg is placed on a rough table. It is connected to a mass of 6 kg by a string that goes over a smooth pulley attached to the edge of the table. The larger mass hangs down freely, just staying in balance. Find the frictional force acting on the lighter object. Then a mass of 4 kg is added to 6 kg. Find the acceleration of the system and the new tension of the string.
5. A mass of 6 kg is placed in the middle of the surface of a table. It is connected to two strings and they were placed over two smooth pulleys that are in opposite ends of the table. One free end of the string is attached to 8 kg and the other end is attached to 2 kg. When the system is released from rest, find the tension of each string and the acceleration.
6. Two smooth planes form an isosceles skeleton with each plane at an angle of 30⁰ to the horizontal. A smooth pulley is fixed at the vertex of the skeleton. A string is placed over the pulley and its free ends are connected to masses of 12 kg and 8 kg. The system is then released from rest. Find the acceleration and the speed after 5 seconds.