Integration - Volume of Revolution

Suppose that f(x) is a function of x and the curve of the function is rotated around the x-axis through 360⁰. It clearly forms a solid object. The volume of the object can be calculated as follows:

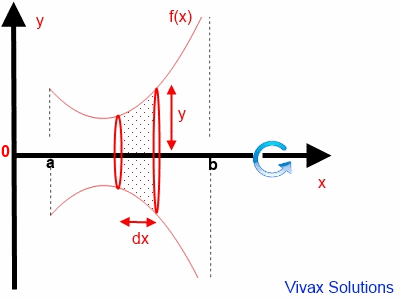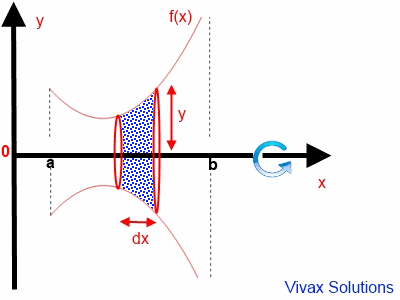
Consider a small disk with thickness dx. If its volume is dv,
dv =π y² dx
dv =π f(x)² dx
In order to find the total volume, V of the object, let's integrate the above between a and b.
V =π _a ∫ ^b f(x)² dx.

So, in order to find the volume of revolution:
1) Square the function and then integrate it
2) Then, multiply the answer byπ

E.g.1

Show that the volume of a cylinder is, V =π r² h.

A cylinder is produced when the line y = r is rotated around x-axis.

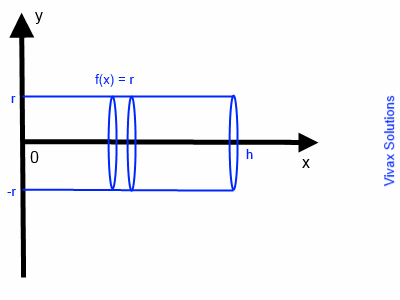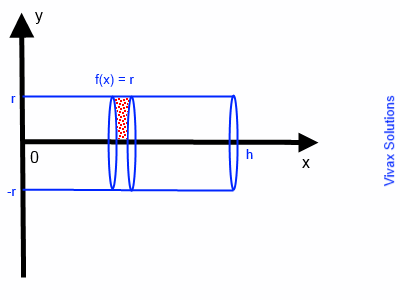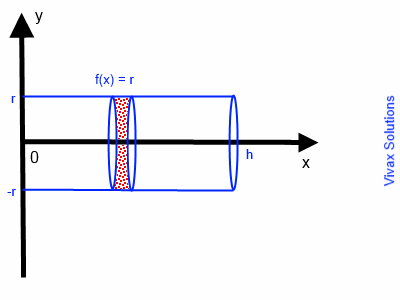
V = π ₀∫^h f(x)² dx
V = π ₀∫^h r² dx
V = π [r²x]^h₀
V =π r² h.

In the following applet, y = 2 line is rotated around the x-axis, shown in red. The y-axis is shown in green. Please press the play button or move the slider. You will see the cylinder being formed.

E.g.2

Show that the volume of a cone is, V = 1/3π r² h.

A cone is produced when a line y = mx is rotated around the x-axis.

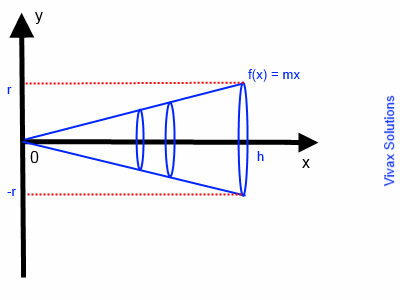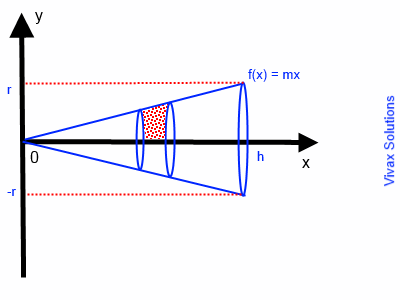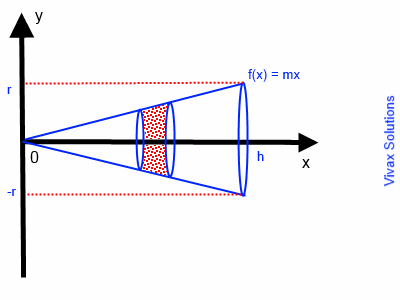
V =π ₀∫^h f(x)² dx
V = π ₀∫^h (mx)² dx
V =π m² ₀ ∫ ^h x² dx
V =π m² [ x³ / 3]₀^h
m, the gradient of the line, = r /h
V =π r² / h² h³ / 3
V = 1/3π r² h

 

In the following applet, y = x line is rotated around the x-axis, shown in red. The y-axis is shown in green. Please press the play button or move the slider. You will see the cone being formed.

 

E.g.3

Show that the volume of a sphere is, V = 4/3π r³.

A sphere is produced when the semi-circle, x² + y² = r² is rotated around the x-axis.

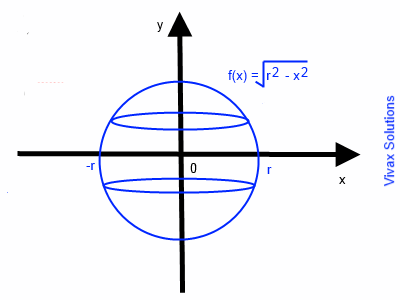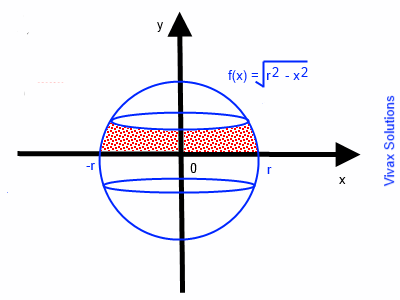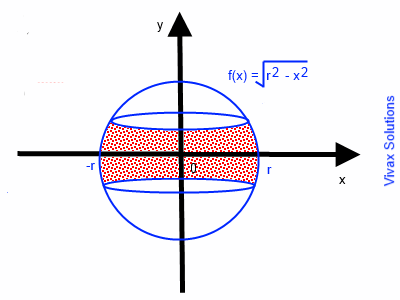
V =π _-r∫^r f(x)² dx
V = π _-r∫^r [ √r² - x² ]² dx
V = π _-r∫^r[r² - x²] dx
V =π [ r²x - x³/3 ]^r_-r
V =π [ r³ - r³/3] - [-r³ - (-r)³/3 ]
V =π [ r³ - r³/3 + r³ - r³/3 ]
V =π [ 2r³ - 2r³ / 3 ]
V = 4/3π r³

In the following applet, the curve, x² + y² = r², is rotated around the x-axis, shown in red. The y-axis is shown in green. Please press the play button or move the slider. You will see the sphere being formed.

 

E.g.4

Find the volume of the object formed when the curve, y = x² + 2 around the x-axis, between x = 0 and x = 3.

A 'vase' is produced when the curve, y = x² + 2 is rotated around the x-axis.

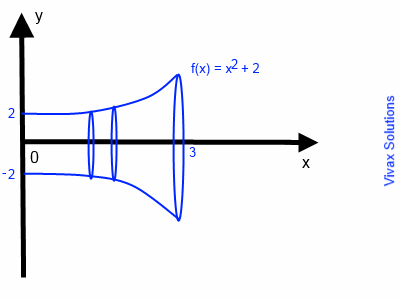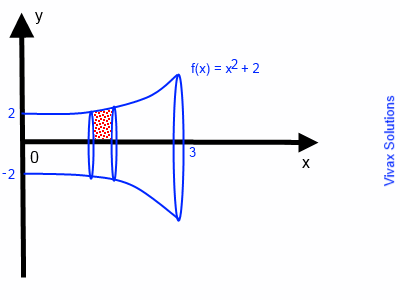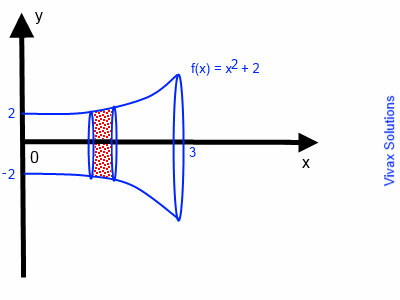
V =π ₀∫³ f(x)² dx
V = π ₀∫³ [ x² + 2 ]² dx
V = π ₀∫³[x⁴ + 4x² + 4] dx
V =π [ x⁵/5 + 4x³/3 + 4x ]³₀
V =π [ 3⁵/5 + 4(3)³/3 + 4(3)] - [0⁵/5 + 4(0)⁰/3 + 4(0) ]
V =π [96.6]
V = 96.6 π
V = 96.6π