The Dot Product - Scalar Product

The dot product of two vectors is defined as follows:

A.B = |A| |B| cos(θ), where |A|, |B| = magnitude of A and B,and θ = angle between the two vectors;

In order to see the impact of the change in angle on the dot product of the two vectors below, please move the slider slowly and see the value.
|A| =4; |B| = 6

 

Angle: 0⁰ 180⁰

 

Since the right hand side of the formula is a number, a scalar, this is also called the scalar product.

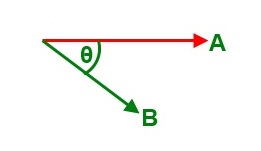
It is important to note that the angle between the two vectors must be considered in the following way:

 

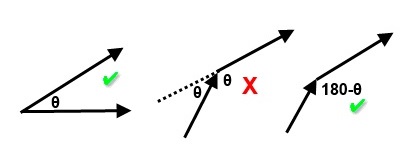
The Dot Product of Unit Vectors

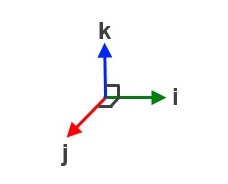
i.j = |i| |j| cos(90)
= 1 X 1 X 0
= 0

i.i = |i| |i| cos(0)
= 1 X 1 X 1
= 1

j.j = |j| |j| cos(0)
= 1 X 1 X 1
= 1

k.k = |k| |k| cos(0)
= 1 X 1 X 1
= 1

i.k = |i| |k| cos(90)
= 1 X 1 X 0
= 0

j.k = |j| |k| cos(90)
= 1 X 1 X 0
= 0

If two vectors are parallel, the dot product is maximum.

If two vectors are perpendicular, the dot product is zero.

 

E.g.1

If a = 2i + 3j -5k and b = 3i - 5j + 4k, find the a.b.

a.b = (2i + 3j -5k).(3i - 5j + 4k)
= 6i.i - 15j.j -20k.k (i.j = j.k = i.k = 0)
= 6 - 15 - 20
= -29.

 

E.g.2

If a = 3i + 2j -5k and b = 4i - 5j + 3k, find the angle between the two vectors.

a.b = (3i + 2j -5k).(4i - 5j + 3k)
= 12i.i - 10j.j -15k.k (i.j = j.k = i.k = 0)
= 12 - 10 - 15
= -23
|a| = √(9 + 4 + 25) = √38; |b| = √(16 + 25 + 9) = √50;
-13 = √38 √50 cos(θ)
cos(θ) = -0.2982
θ = 107.34

 

 

Dot Product Practice

Please move the vectors and see how the dot product varies with the angle or the magnitudes of the vectors.

 

 

E.g.3

Using the dot product, verify that Pythagoras Theorem is true.

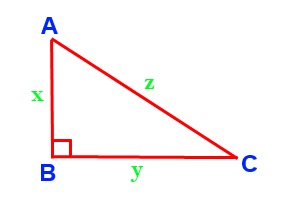
AC.AC= (AB + BC).(AB + BC)
AC.AC= AB.AB + AB.BC + BC.AB + BC.BC
z z cos(0) = x x.cos(0) + x y cos(90) + x y cos(90) + y y cos(0)
z² = x² + 0 + 0 + y²
z² = x² + y²
This is Pythagoras Theorem.

 

E.g.4

Using the dot product, verify the cosine rule.

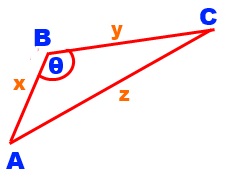
AC.AC= (AB + BC).(AB + BC)
AC.AC= AB.AB + AB.BC + BC.AB + BC.BC
z z cos(θ) = x x.cos(θ) + x y cos(180-θ) + x y cos(180-θ) + y y cos(θ)
z² = x² - xy cos(θ) - xy cos(θ) + y²
z² = x² + y² - 2xy cos(θ)
This is the cosine rule.

 

E.g.5

Using the dot product, prove that the angle of a semi-circle is a right angle.

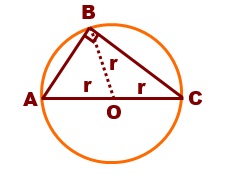
AB.BC= (AO + OB).(BO + OC)
= AO.BO + AO.OC + OB.BO + OB.OC
= r r.cos(180-θ) + r r cos(0) + r r cos(180) + r r cos(θ)
= -r² cos(θ) + r² - r² + r² cos(θ)
= 0
Since the dot product of AB and BC is zero, AB is perpendicular to BC.

Challenge:

Using the dot product, show that the diagonals of a square intersect at right angles.