The specification of GCSE has changed dramatically: first of all, students who sit for GCSE as from 2017 onwards, are going to be tested for four and half hours to earn their grade - from 9 to 1; it used to be just three hours. There are going to face 3 papers, each lasting 1 hour 30 minutes: one non-calculator paper and two calculator papers.
Edexcel, a major examination board in the UK, has updated its specification as follows:
With the introduction of new topics, the examination boards collectively deal with the criticism that they used to face over what critics term, falling standard in mathematics in the UK. Not only will this enhance the standard as a whole, but also bridge the gap between the GCSE and A Level in a constructive way, making the transition for the prospective students smooth.
Do you need a book that explains the above topics in detail - with lots of worked examples? Here is the book written by the developer of this website, available on Amazon:
For any further inquiries, please email: we will get back to you as soon as possible.
E.g.
A straight line passes through (2,5) and (4, 11). Find its equation.
m = (11 - 5) / (4 - 2) = 6 / 2 = 3
y = mx + c
x = 2, y = 5, m = 3,
5 = 3 X 2 + c
5 = 6 + c
c = -1
The equation is y = 3x - 1.
E.g.
The equation of a straight line is y = 2x - 6. Find the coordinates of the point where it crosses the axes at.
When it crosses the x-axis, y = 0
0 = 2x - 6 => x = 3
(3,0)
When it crosses the y-axis, x = o
y = 2X0 -6 => y = -6
(0,-6)
Functions - f(x)
An expression of a variable is called a function of the variable.
For instance, if y = 2x - 3, which is a function of x, it can be written as follows in function form.
f(x) = 2x -3, which is read as f of x equals 2x - 3.
So, any value that you use within the brackets, replaces the x value on the right hand side. The following example shows it in detail:
f(x) = 2x - 3
f(2) = 2 X 2 - 3 = 1
f(0) = 2 X 0 - 3 = -3
f(-2) = 2 X -2 - 3 = -7
f(x + 1) = 2(x + 1) - 3 = 2x + 2 - 3 = 2x - 1
f(x - 1) = 2(x - 1) - 3 = 2x - 2 - 3 = 2x - 5
f(x/2) = 2(x/2) - 3 = x - 3
f(3x) = 2(3x) - 3 = 6x - 3
Gradients of Curves
Unlike straight lines, the gradient of a curve changes with the point in question. For instance, the gradient of the following quadratic curve, a parabola,
is changing from point to point: the gradient at the lowest point, for example, is zero, as it remains flat. The gradient of the curve on the negative x-axis
is negative and on the positive x-axis positive.
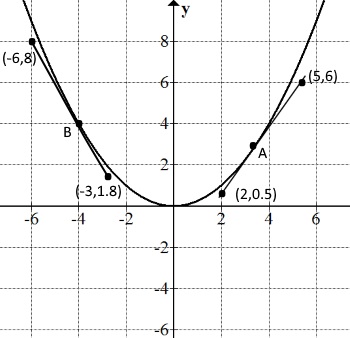
In this case, in order to find the gradient at a specific point, we have to draw a tangent - a line that touches the curve, only at one point.
Of course, drawing a tangent is not easy; nor is it going to be perfect, even if we make a few attempts.
Once a tangent is drawn at the specific point, we find its gradient and take it as the gradient of the curve at the point.
Let's find the gradient of the above curve at A and B respectively.
At A, gradient of the tangent = (6 - 0.5)/(5 - 2) = 5.5/3 = 1.8
So, the gradient of the curve where x = 3 is 1.8
At B, gradient of the tangent = (8 - 1.8)/(-6 - -3) = 6.2/-3 = -2.1
So, the gradient of the curve where x = -4 is -2.1
In this way, we can find the gradient of any point on the curve.
E.g.
Find the nth term of the sequence, 3, 4, 6, 9, 13...
The differences between the consecutive terms of the above: 1, 2, 3, 4
The differences between the consecutive terms: 1, 1, 1 of the above
So, the sequence is quadratic.
Let the nth term, N = an2 + bn + c, where a, b and c are constants to be found.
Since there are three unknowns, we need to make three equations.
n = 1; N = 3 => 3 = a + b + c
n = 2; N = 4 => 4 = 4a + 2b + c
n = 3; N = 6 => 6 = 9a + 3b + c
From the first two, we get:
1 = 3a + b
From the last two, we get:
2 = 5a + b
By solving the simultaneous equations, we get,
a = 1/2 and b = -1/2; sub them in the first equation,
c = 3
So, N = (1/2)n2 - (1/2)n + 3.
There are many more worked examples, covering all the new topics.. The book will guide you through all that is needed to master the new, advanced topics.
It's a complete reference material for the new topic of GCSE(9 - 1) - with plenty of worked problems in each topic.