Simultaneous Equations - interactive practice

In this tutorial, you will learn how to solve simultaneous equations by:

Equations that must be solved at the same time are simultaneous equations. They have two unknowns.

E.g.
2x + 3y = -9
x + 4y = 6

We use three different methods to solve simultaneous equations. They are:

1. Elimination method
2. Substitution method
3. Graphical method
4. Matrix method

Elimination Method

In this method, we must get rid of one variable in order to find the other.

E.g.1

x + y = 6 1
x - y = 2 2
If we add the two equations, we can remove y.
1 + 2 => 2x = 8
x = 4
Sub in 1 => 4 + y = 6
y = 2
Solutions are x = 4 and y = 2.

E.g.2

2x + y = 6 1
3x - 2y = 2 1
To remove y, multiply the first equation by 2 and then add the two equations together.
1 X 2 => 4x + 2y = 123
2 + 1 => 7x = 14
x = 2
Sub in 1
4 + y = 6
y = 2
The solutions are x = 2 and y = 2.

E.g.3

2x + 3y = 1 1
3x - 2y = 8 2
In this case, to eliminate y, the first equation must be multiplied by 2 and the second equation must be multiplied by 3.
1 X 2 => 4x + 6y = 2 3
2 X 3 => 9x - 6y = 24 4
3 + 4 => 13x = 26
x =2
Sub in 1=> 4 + 3y = 1
-4 => 3y = -3
y = -1
The solutions are x = 2 and y = -1.

Substitution Method

We get y in terms of x or vice versa from one equation, and put that in the other.

E.g.1

x + y = 6 1
x - y = 2 2
From 1 => x = (6 - y)
Sub this in 2 => 6 - y - y = 2
6 - 2y = 2
-6 => -2y = -4
:--2 => y = 2
Sub in 1 => x + 2 = 6
x = 4
Solutions are x = 4 and y = 2.

E.g.2

2x + y = 6 1
3x - 2y = 2 2
From 1 => y = (6 - 2x)
Sub this in 2 => 3x - 2(6 - 2x) = 2
3x - 12 + 4x = 2
7x - 12 = 2
+ 12 => 7x = 14
x = 2
Sub in 1 => 4 + y = 6
-4 => y = 2
The solutions are x = 2 and y = 2.

E.g.3

2x + 3y = 1 1
3x - 2y = 8 2
From 1 - 3y => 2x = (1 - 3y)
x = (1 - 3y)/2
Sub in 2 => 3(1 - 3y)/2 - 2y = 8
X 2 => 3(1 - 3y) - 4y = 16
3 - 9y - 4y = 16
3 - 13y = 16
-3 => -13y = 13
y = -1
Sub in 1 => 2x - 3 = 1
+ 3 => 2x = 4
x = 2
The solutions are x = 2 and y = -1.

Graphical Method

In this method, two straight lines are drawn for each equation. Then the point where the two lines intersect at is noted. The coordinates of this point are the solutions of the equations.

E.g.1

2x + y = 8 1
y -x = 1 2
1 => y = 8 - 2x
2 => y = x + 1

x	y = 8 - 2x
0	8
-1	10
2	4

x	y = x + 1
0	1
-1	0
2	3

Rearrange the two equations in the form of y = mx + c and draw two lines for them on the same grid.

 

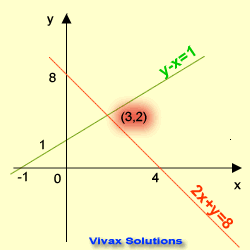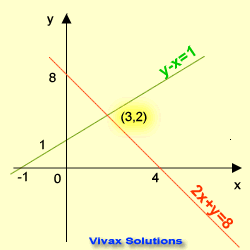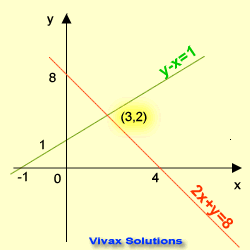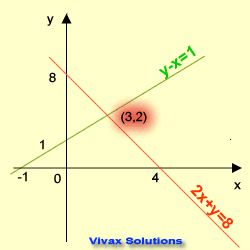
The coordinates of the point of intersection are x = 3 and y = 2.
So, the solutions are x = 3 and y = 2.

Matrix Method

This is ideal for those who do Further Mathematics(FP1) at A-Level. Matrices is part of Further Mathematics Syllabus. It is useful for advanced mathematics too.

In this method, the inverse matrix of the matrix P must be found first. Then, matrix, Q, which gives the values of x and y could be found by matrix multiplication. The following image clearly shows how it is done.

The method can be extended to solve any pair simultaneous equations; all you have to do is rearranging them in matrix form.

 

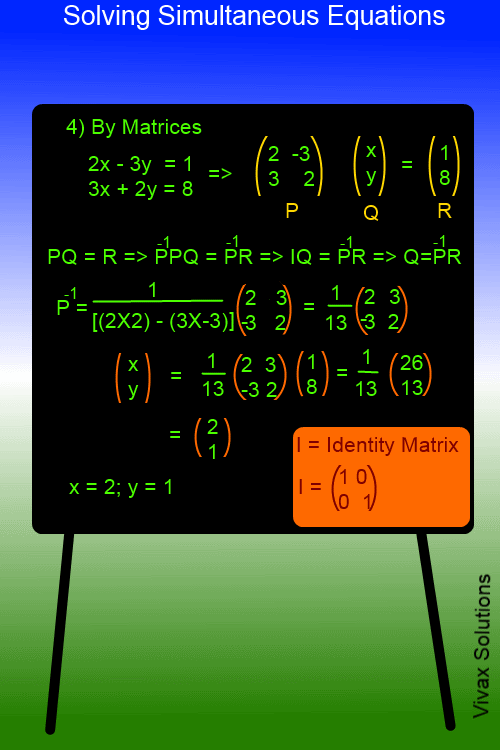
Now, in order to complement what you have just learnt, work out the following questions:

 

Algebra Equation Generator

You can generate as many questions as you want with the following programme, along with the answers. First generate the question, then work them out and check with the answer.