Stem and Leaf Diagrams
Stem and Leaf diagrams provide a way to show data as it is done in tables and charts. It is ideal to represent a large number of data so that we can get a clear idea about the spread and peaks
at a glance. In addition, the averages can be calculated speedily too.
The Marks for English Literature in a certain GCSE class is as follows; the corresponding stem and leaf diagram is on the right:
15,32,39,54,55,79
77,99,52,37,34,56
35,13,18,19,90,59
12,34,37,75,53,34
10.59,70,95,33,12
4|3 means 43
The mode of the data = 34
The median of the data = 30/2 = 15th value = 37
The mean of the data = 45.2
The above Stem and Leaf diagram can be extended to show two different sets of data on either side - of the stem. The it is called Back-to-Back Stem and Leaf Diagram.
E.g.
The Marks for English Literature in two GCSE classes are as follows; the corresponding Stem and Leaf diagrams are on the right:
Class 1 - on the right
15,32,39,54,55,79
77,99,52,37,34,56
35,13,18,19,90,59
12,34,37,75,53,34
10.59,70,95,33,12
Class 2 -on the left
16,33,38,55,56,78
78,98,53,36,35,57
36,14,19,18,91,58
13,35,38,76,54,35
11.58,71,96,34,13
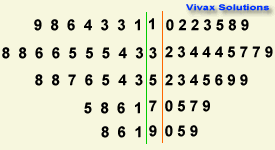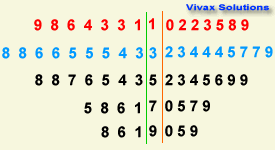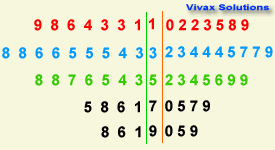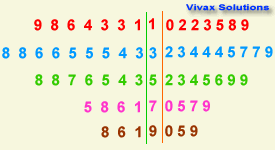2|4|3 means 42 on the left and 43 on the right
The mode of class 1 = 34
The median of class 1 = 30/2 = 15th value = 37
The mean of class 1 = 45.2
The mode of class 2 = 35
The median of class 2 = 30/2 = 15th value = 38
The mean of class 2 = 46.6
Stem and Leaf Diagrams - interactive practice
With the following applet, you can practise stem and leaf diagrams interactively. All you have to do is clicking the button to generate a random set of data.
Practice Questions
- The temperature in March, in Middlesex area is as follows:
12, 9, 9, 21, 10, 7, 8, 11, 10, 15, 14, 13, 12,9, 14
11, 10, 19, 11, 20, 17, 18, 11, 10, 13, 12, 11, 12,9, 11
Construct a Stem and Leaf diagram to find the averages of the data.
- The heights of two sets of plants - one grown with a special fertilizer and the other one without - are as follows:
Set A
23, 32, 42, 14, 16, 32, 33, 16, 15, 22, 51, 28, 56, 27, 29
26, 38, 13, 24, 26, 11, 15, 19, 18, 32, 46, 52 26, 57, 59
23, 32, 42, 24, 16, 22, 33, 26, 15, 22, 51, 28, 56, 27, 29
46, 38, 13, 24, 26, 21, 35, 19, 48, 32, 46, 22 26, 57, 59
Set B
13, 32, 32, 14, 16, 32, 33, 26, 25, 22, 51, 28, 56, 27, 29
26, 38, 13, 24, 26, 11, 55, 29, 18, 32, 46, 52 46, 57, 59
23, 32, 42, 24, 26, 22, 33, 26, 15, 22, 51, 38, 46, 27, 29
46, 38, 13, 24, 16, 21, 35, 29, 48, 42, 46, 22 26, 57, 59
Construct a back-to-back Stem and Leaf diagram to calculate the averages for both groups.