Solving Trigonometric Equations

E.g.1

 

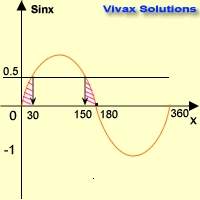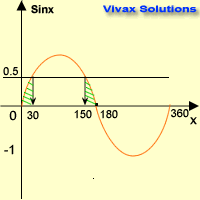
Solve sin x = 0.5 for 0 ≤ x ≤ 360
sin x = 0.5
x = 30⁰
Since y = 0.5 line crosses the sine curve at two points, there are two solutions.
Now, look at the symmetry of the graph; the two values of x are 30⁰ and 150⁰.
x = 30 and 150.

E.g.2

 

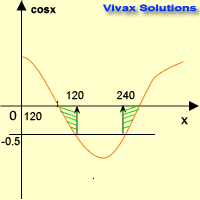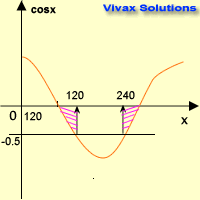
Solve cos x = -0.5 for 0 ≤ x ≤ 360
cos x = -0.5
x = 120⁰
Since y = -0.5 line crosses the sine curve at two points, there are two solutions.
Now, look at the symmetry of the graph; the two values of x are 120⁰ and 240⁰.
x = 120 and 240.

E.g.3

Solve sin (x +10) = 0.5 for 0 ≤ x ≤ 360
From example 1,
(x + 10) = 30⁰
There are two values for (x +10) that satisfy the equation; they are 30⁰ and 150⁰
x + 10 = 30 or x + 10 = 150
x = 20 or x = 140

E.g.4

Solve 1 + 2 sin x = 2 for 0 ≤ x ≤ 360
2 sin x = 1
sin x = 0.5
From example 1,
x = 30⁰
There are two values for x that satisfy the equation; they are 30⁰ and 150⁰
x = 30 or x = 150.

Solving Equations - interactive

You can animate the y=a line by clicking the play button or move the slider to a point you want it to be at.

 

Now, in order to complement what you have just learnt, work out the following questions:

1. Solve 2 sin x = 1.5 for 0 ≤ x ≤ 360
2. Solve 1 + 3 cos x = 2 for 0 ≤ x ≤ 360
3. Solve sin (2x - 10) = 0.7 for 0 ≤ x ≤ 360
4. Solve tan (x -30) = 0.7 for 0 ≤ x ≤ 360
5. Solve cos (2x -20) = 0.5 for 0 ≤ x ≤ 360
6. Solve sin² x = 0.25 for 0 ≤ x ≤ 360
7. Solve sin 2x = 0.5 for 0 ≤ x ≤ 360
8. Solve 1 + 3 sin 2x = 2 for 0 ≤ x ≤ 360