Basic Trigonometry

There are three basic trigonometric functions defined for a right-angled triangle:

1. sine
2. cosine
3. tan

Let a, and b be the two sides and c be the hypotenuse. Then the functions takes the following form:

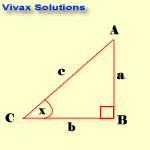
• sin x = opposite / hypotenuse = a /c
• cos x = = adjacent / hypotenuse = b / c
• tan x = opposite / adjacent = a / b

The following examples are based on this triangle.

E.g.1

In the above triangle, AB = 3cm and x = 30⁰. Find AC and BC.
sin 30 = 3 /AC
0.5 = 3 / AC
AC = 6cm.
cos 30 = b /AC
0.8660 = b / 6
AC = 5.1cm.

E.g.2

In the above triangle, BC = 4cm and x = 60⁰. Find AC and AB.
cos 60 = 4 /AC
0.5 = 4 / AC
AC = 8cm.
tan 60 = AB /BC
1.7 = AB / 4
AB = 6.8cm.

E.g.3

In the above triangle, AB = 3cm and BC = 5cm. Find x.
tan x = 3 / 5 = 0.6
x = tan^-10.6 = 28.6
x = 28.6⁰

 

The Sine Rule

 

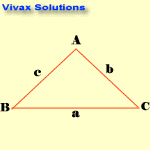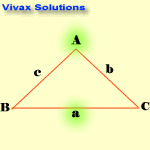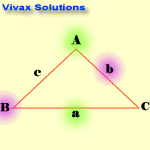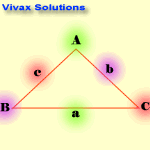
sin A / a = Sin B /b = Sin C /c

Note the blinking letters to see the relationship.

E.g.1

A = 30⁰ ; B = 50⁰; b = 9cm; find c.
c / sin 50 = 9 / sin 30
c = 9 x sin 50 / sin 30
c = 13.7 cm.

E.g.2

A = 110⁰ ; b = 5cm; a = 9cm; find B.
5 / sin B = 9 / sin 110
sin B = 5*sin 110 / 9
B = 31.5⁰

The Cosine Rule

 

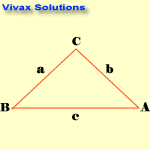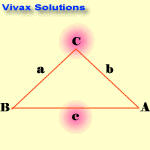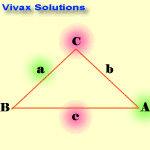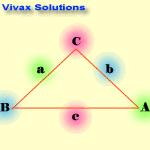
c² = a² + b² - 2abcosC

Note the blinking letters to see the relationship.

E.g.1

a = 4cm; b =5cm and C = 60⁰; find c.
c² = 4² + 5² - 2x4x5xcos60
c² = 16 + 25 - 20
c² = 21
c= 4.6 cm.

E.g.2

a = 5cm; b = 12cm and C = 90⁰; find c.
c² = 5² + 12² - 2x5x12xcos90
c² = 25 + 144 - 0
c² = 169
c= 13cm.

E.g.3

a = 8cm; b =7cm and C = 120⁰; find c.
c² = 8² + 7² - 2x8x7xcos120
c² = 64 + 49 + 56
c² = 169
c= 13 cm.

E.g.4

a = 7cm; b= 6cm; c = 8 cm; find C.
8² = 7² + 6² - 2x4x5xcosC
64 = 49 + 36 - 84cosC
-84cosC = -21
cosC = 0.25
C = 75.5⁰

Area of a Triangle

 

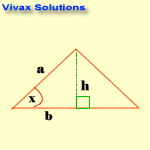
A = 1/2 absinx

Proof:
A = 1/2 X h X b
sin x = h / a => h = a sinx
A = 1/2 absinx

E.g.

a = 4cm; b= 8cm; x = 30⁰
A = 1/2 * 4 * 8 * sin 30
A = 8cm².

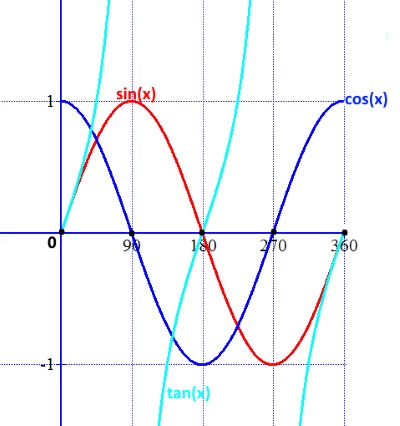
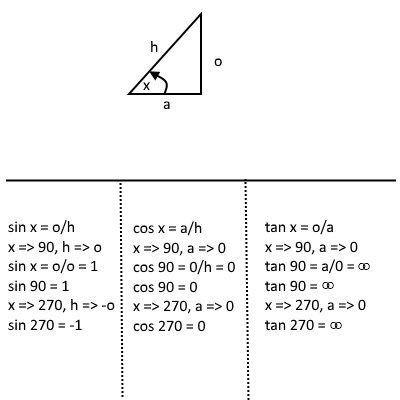
Deriving Trigonometric Values of 0⁰, 30⁰, 45⁰, 60⁰, 90⁰, 180⁰, 360⁰

Trigonometric values of major angles, such as 0⁰, 90⁰, 180⁰, 270⁰ and 360⁰ can be remembered with the aid of the trigonometric curves, if you can visualize them. The three major curves are as follows:

The following image shows how to obtain the values of 0⁰, 180⁰, and 360⁰ from the basic definitions

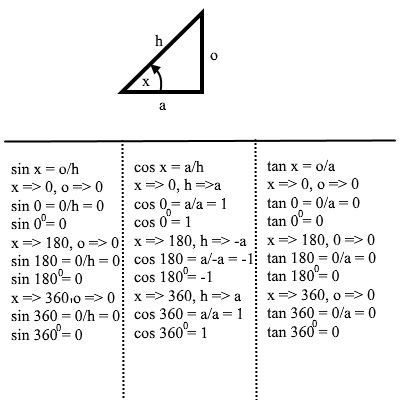
The following image shows how to obtain the values of 90⁰ and 270⁰ from the basic definitions

In addition, the values of 30⁰, 45⁰ and 60⁰ can be derived in the following way:

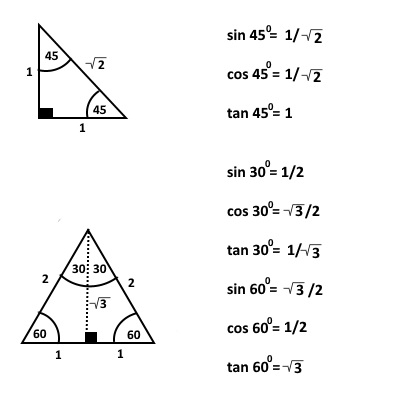
The trigonometric values of 45⁰ is calculated from an right-angled isosceles triangle with each equal side being 1 unit.
The values of 30⁰ and 60⁰ are calculated from an equilateral triangle of each side 2 unit.

Trigonometric Values in the Four Quadrants

The angles are measured from the border between the first and the fourth quadrants - and anticlockwise, by convention. If it is measured in clockwise, it is considered as negative.

The following animation explicitly demonstrates it:

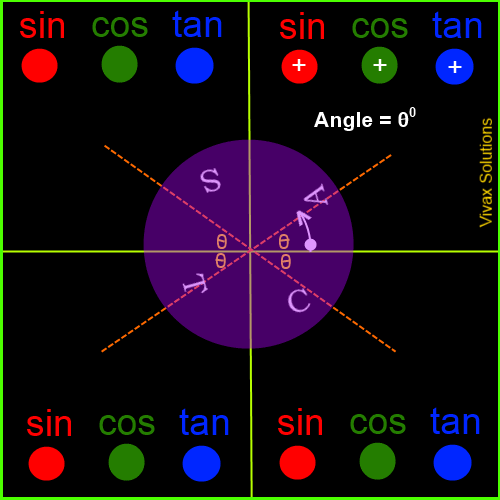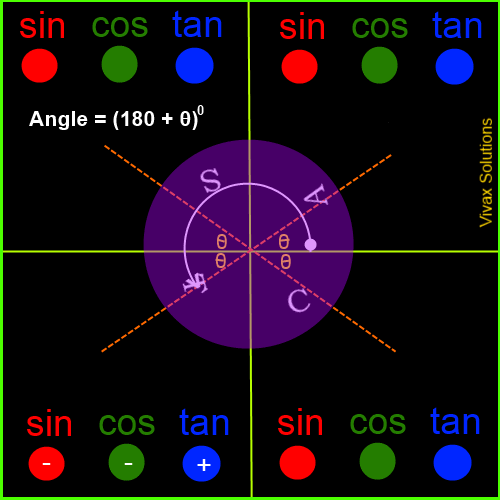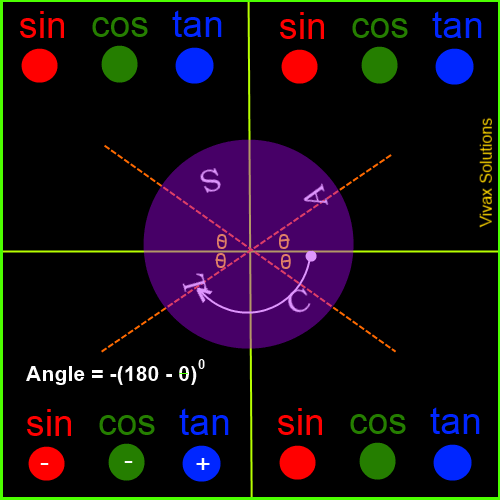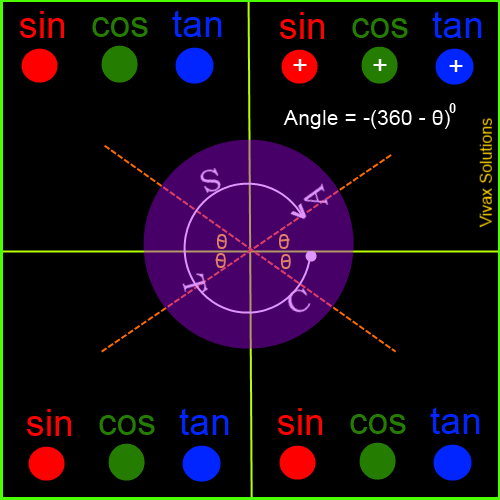
Now, in order to complement what you have just learnt, work out the following questions:

1. ABC is a triangle. AB = 6cm and angle ABC = 45⁰. Find the perimeter and the area of the triangle.
2. Prove that Pythagoras Theorem is correct using the Cosine Rule.
3. The height of a man is 1.2m. When he looks at the top of a tree, standing 20m away from it, the angle of elevation is 32⁰. Calculate the height of the tree.
4. Points P and Q are due south and West of a pillar of height 20m. The angle of elevation of the top from these points are 22⁰ and 42⁰ respectively. Find the distance between P and Q.
5. A ship is sailing a distance of 200 miles from port X to port Y, on a bearing 020⁰. At Y, it changes its course on a bearing 110⁰ and reaches port Z, after travelling 360 miles. Find the distance between port X and Port Z. Find the bearing of Z from X as well.
6. A jet is flying a distance of 120 miles from town P to town Q, on a bearing 030⁰. At Q, it changes its course on a bearing 60⁰ and reaches town R, after travelling 240 miles. Find the distance between town P and town R. Find the bearing of R from P as well.
7. A man is looking down from a cliff at another man on the beach. The angle of depression is 20⁰. The second man walks 200m away from the cliff and the new angle of depression for the man at the top becomes 15⁰. Find the vertical height of the cliff.
8. The two sides of a right-angled triangle are 5cm, 12cm. Find its size of hypotenuse and the rest of the angles of the triangle.
9. The three sides of a triangle are 8cm, 7cm and 13cm. Find its area. Calculate the shortest distance between a vertex and the longest side as well.
10. ABC is a triangle with AB = 4cm and AC = 5cm. AD is at an right angle to BC. AD = 3cm. Find BC.