Interactive Algebraic Practice for GCSE & iGCSE - AQA, Edexcel and OCR

This is an interactive tutorial for you to master every major algebraic topic that comes in both GCSE and iGCSE specifications. In most topics, you can generate questions at random, work them out and then check the answers too.

The topics covered are as follows:

Simple Equations

 

An equation is almost a sort of seesaw: you add something to the left, lose the balance and are forced to do the same to the right; you divide and multiply by something, once again, the same must be done to the other side; if you subtract something, there is no exception. Therefore, solving equation means, getting rid of everything around x by seesaw method.

E.g.1

x + 5 = 8
- 5 => x + 5 -5 = 8 - 5
x = 3

E.g.2

x - 5 = 10
+ 5 => x -5 + 5 = 10 + 5
x = 15

E.g.3

2x = 10
:- 2 => 2x / 2 = 10 /2
x = 5

E.g.4

x / 5 = 2
X 5 => x /5 X 5 = 2 X 5
x = 10

E.g.5

2x - 4 = 10
+ 4 => 2x - 4 + 4 = 10 + 4
2x = 14
:- 2 => 2x / 2 = 14 / 2
x = 7

E.g.6

2x + 4 = 10
- 4 => 2x + 4 - 4 = 10 - 4
2x = 6
:- 2 => 2x / 2 = 6 / 2
x = 3

E.g.7

x/3 + 7 = 10
-7 => x/3 + 7 - 7 = 10 - 7
x/3 = 3
X 3 => x/3 X 3 = 3 X 3
x = 9

E.g.8

(x - 3) / 4 = 3
X 4 => (x-3) /4 X 4 = 3 X 4
(x-3) = 12
+ 3 => x - 3 + 3 = 12 + 3
x = 15

E.g.9

3x + 3 = x + 10
-3 => 3x + 3 -3 =x + 10 - 3
3x = x + 7
- x => 3x - x = x - x + 7
2x = 7
:-2 => 2x / 2 = 7 / 2
x = 3.5

E.g.10

2x - 4 = 5x + 8
+4 => 2x - 4 + 4 = 5x + 8 + 4
2x = 5x + 12
-5x => 2x - 5x = 5x - 5x + 12
-3x = 12
:--3 => -3x/-3 = 12 / -3
x = -4

 

Simple Equation Generator

With this simple programme, you can generate questions at random, along with answers - unlimited number of questions. Generate the question first, work out the solution and then check with the answer shown below the question.

 

Hard Equations

E.g.1

2(x + 5) = 18
:- 2 => 2(x + 5) :- 2 = 18 :- 2
x + 5 = 9
- 5 => x + 5 - 5 = 9 - 5
x = 4

E.g.2

5(x - 2) = 2(x - 3)
5x - 10 = 2x - 6
+10 => 5x - 10 + 10 = 2x - 6 + 10
5x = 2x + 4
-2x => 5x - 2x = 2x - 2x + 4
3x = 4
:-3 => 3x / 3 = 4 /3
x = 1.3

E.g.3

4(x + 4) + 3(x -3) = 2(x -3) + 12
4x + 16 + 3x - 9 = 2x - 6 + 12
7x + 7 = 2x + 6
- 7 => 7x + 7 - 7 = 2x + 6 - 7
7x = 2x - 1
-2x => 7x - 2x = 2x - 2x -1
5x = -1
:-5 => 5x / 5 = -1 / 5
x = -0.2

E.g.4

(x + 5) / 4 = (x -3) / 2
X 4 => 4 X (x + 5) /4 = 4 X (x- 3) / 2
(x + 5) = 2 (x -3)
x + 5 = 2x - 6
- 5 => x +5 -5 = 2x - 6 - 5
x = 2x - 11
-2x => x - 2x = 2x - 2x -11
-x = -11
-1 X x = 11

E.g.5

3 + 2(x + 5) = 3 - (2x - 1)
3 + 2x + 10 = 3 -2x + 1
13 + 2x = 4 - 2x
-13 => 2x + 13 - 13 = 4 - 2x - 13
2x = -2x - 9
+2x => 2x + 2x = 2x - 2x - 9
4x = -9
:- 4 => 4x / 4 = -9 / 4
x = -2.25

 

Hard Equation Generator

With this simple programme, you can generate questions at random, along with answers - unlimited number of questions. Generate the question first, work out the solution and then check with the answer shown below the question.

 

Algebraic Equations - word problems

These are a set of problems that you can solve algebraically. Form the equation from the description and then solve it.

E.g.1

I think of a number, add 7 and the answer is 10. Find the number.
Let the number be x.
x + 7 = 10
-7 => x + 7 -7 = 10 -7
x = 3
The number is 3.

E.g.2

I think of a number, take away 5 and the answer is 10. Find the number.
Let the number be x. x - 5 = 10
+ 5 => x -5 + 5 = 10 + 5
x = 15
The number is 15.

E.g.3

I think of a number, multiply by 3 and the answer is 30. Find the number.
Let the number be x.
3x = 30
:- 3 => 3x / 3= 30 /3
x = 10
The number is 10.

E.g.4

I think of a number, multiply it by 2, take away 4. The answer is 10. Find the number.
Let the number be x. 2x - 4 = 10
+ 4 => 2x - 4 + 4 = 10 + 4
2x = 14
:- 2 => 2x / 2 = 14 / 2
x = 7
The number is 7.

E.g.5

I think of a number, divide by three, add 7. The answer is 10. Find the number.
Let the number be x. x/3 + 7 = 10
-7 => x/3 + 7 - 7 = 10 - 7
x/3 = 3
X 3 => x/3 X 3 = 3 X 3
x = 9
The number is 9.

E.g.6

I think of a number, take away three and then divide by 4. The answer is 3. Find the number.
Let the number be x.
(x - 3) / 4 = 3
X 4 => (x-3) /4 X 4 = 3 X 4
(x-3) = 12
+ 3 => x - 3 + 3 = 12 + 3
x = 15
The number is 15.

E.g.7

I think of a number, multiply by 3, add 3. The answer is the same, if I add 10 to the number. Find the number.
Let the number be x.
3x + 3 = x + 10
-3 => 3x + 3 -3 =x + 10 - 3
3x = x + 7
- x => 3x - x = x - x + 7
2x = 7
:-2 => 2x / 2 = 7 / 2
x = 3.5
The number is 3.5.

E.g.8

I think of a number, multiply by 2, take away 4. The answer is the same if I multiply it by 5 and then add 8. Find the number.
Let the number be x.
2x - 4 = 5x + 8
+4 => 2x - 4 + 4 = 5x + 8 + 4
2x = 5x + 12
-5x => 2x - 5x = 5x - 5x + 12
-3x = 12
:--3 => -3x/-3 = 12 / -3
x = -4
The number is -4.

E.g.9

The width of a rectangle is 2cm less than the length. The perimeter is 20 cm. Find the length and the area.
let the width be x. So, the length = x + 2.
x + x + 2 + x + x + 2 = 20
4x + 4 = 18
-4 => 4x + 4 - 4 = 20 - 4
4x = 16
:-4 => 4x / 4 = 16 / 4
x = 4
Width = 4cm; length = 6cm;
Area = 24 cm².

E.g.10

The sum of two consecutive odd numbers is 52. Find the numbers.
Let the first number be x. Then the next one is x + 2.
x + x + 2 = 52
2x + 2 = 52
-2 => 2x + 2 - 2 = 52 - 2
2x = 50
:-2 => 2x / 2 = 50 / 2
x = 25
The numbers are 25 and 27.

This is the book on the new GCSE Mathematics 9-1 Topics: lots of worked examples for progressive training

 

Practice Questions

Now, in order to complement what you have just learnt, work out the following questions:

1. I think of a number, multiply by 4 and add 5. The answer is 29. Find the number.
2. I think of a number, add 3 and the result is multiplied by 4. The answer is 28. Find the number.
3. I think of a number, add 6 and divide by 3. The answer is 5. Find the number.
4. I think of a number, multiply by 4, and add 6. The result is then multiplied by 5 and the answer is 70. Find the number.
5. Twice a number added to 5 is the same as the number added to 10. Find the number.
6. A number multiplied by 5, add 4 is the same as 6 times the number. Find the number.
7. Three times a number, add nine, divided by 6 is the same as the number itself. Find the number.
8. Twice a number added to 6 is the same as ten subtracted from six times the number. Find the number.
9. The sum of three consecutive numbers is 78. Find the numbers.
10. The sum of three consecutive even numbers is 60. Find the numbers.
11. The sum of the half, the third and the forth of a number is 10 more than the original number. Find the number.
12. The sixth of a number exceeds the eight of the same number by 4. Find the number.
13. Divide £110 among Amy, Basil and Clare in such a way that Amy has £10 more than Basil and Basil has £20 more than Clare.
14. Find a number so that its half exceeds the sum of the fifth and the sixth of the same by 16.
15. A man is twice old as his son is now. Eighteen years ago, he was 5 times as old as his son was then. How old is his son now?
16. The length of a plank of wood is 2cm more than its width. If the length and width were 1cm and 3cm more, the plank would have been a square. Find the length and width of the plank.
17. Anil and Bimal shared £80 between them. When Bimal gives Anil £20, Anil has £12 more than Bimal. How much did then have at the beginning?
18. The sum of two numbers is 112. Find the numbers, if the difference between them is 48.
19. Find two numbers with a difference and a mean, 8 each.
20. The longest side of an isosceles triangle is 4cm more than the twice of each other side. Find the length of the longest side, if the perimeter is 44cm.

 

Answers

Move the mouse over, just below this, to see the answers:

1. 6
2. 4
3. 9
4. 2
5. 5
6. 4
7. 3
8. 4
9. 25, 26, 27
10. 18, 20, 22
11. 120
12. 96
13. 50, 40, 20
14. 120
15. 24
16. 6, 4
17. 26, 54
18. 80, 32
19. 12, 4
20. 24

 

Simultaneous Equations

Equations with two unknowns are called simultaneous equations. In order to solve them, they must be boiled down to a single equation, a linear one, first, and then solve it. Here are some methods and worked examples for you to follow them.

Elimination Method

In this method, we must get rid of one variable in order to find the other.

E.g.1

x + y = 6 1
x - y = 2 2
If we add the two equations, we can remove y.
1 + 2 => 2x = 8
x = 4
Sub in 1 => 4 + y = 6
y = 2
Solutions are x = 4 and y = 2.

E.g.2

2x + y = 6 1
3x - 2y = 2 1
To remove y, multiply the first equation by 2 and then add the two equations together.
1 X 2 => 4x + 2y = 123
2 + 1 => 7x = 14
x = 2
Sub in 1
4 + y = 6
y = 2
The solutions are x = 2 and y = 2.

E.g.3

2x + 3y = 1 1
3x - 2y = 8 2
In this case, to eliminate y, the first equation must be multiplied by 2 and the second equation must be multiplied by 3.
1 X 2 => 4x + 6y = 2 3
2 X 3 => 9x - 6y = 24 4
3 + 4 => 13x = 26
x =2
Sub in 1=> 4 + 3y = 1
-4 => 3y = -3
y = -1
The solutions are x = 2 and y = -1.

Substitution Method

We get y in terms of x or vice versa from one equation, and put that in the other.

E.g.1

x + y = 6 1
x - y = 2 2
From 1 => x = (6 - y)
Sub this in 2 => 6 - y - y = 2
6 - 2y = 2
-6 => -2y = -4
:--2 => y = 2
Sub in 1 => x + 2 = 6
x = 4
Solutions are x = 4 and y = 2.

E.g.2

2x + y = 6 1
3x - 2y = 2 2
From 1 => y = (6 - 2x)
Sub this in 2 => 3x - 2(6 - 2x) = 2
3x - 12 + 4x = 2
7x - 12 = 2
+ 12 => 7x = 14
x = 2
Sub in 1 => 4 + y = 6
-4 => y = 2
The solutions are x = 2 and y = 2.

E.g.3

2x + 3y = 1 1
3x - 2y = 8 2
From 1 - 3y => 2x = (1 - 3y)
x = (1 - 3y)/2
Sub in 2 => 3(1 - 3y)/2 - 2y = 8
X 2 => 3(1 - 3y) - 4y = 16
3 - 9y - 4y = 16
3 - 13y = 16
-3 => -13y = 13
y = -1
Sub in 1 => 2x - 3 = 1
+ 3 => 2x = 4
x = 2
The solutions are x = 2 and y = -1.

Graphical Method

In this method, two straight lines are drawn for each equation. Then the point where the two lines intersect at is noted. The coordinates of this point are the solutions of the equations.

E.g.1

2x + y = 8 1
y -x = 1 2
1 => y = 8 - 2x
2 => y = x + 1

x	y = 8 - 2x
0	8
-1	10
2	4

x	y = x + 1
0	1
-1	0
2	3

Rearrange the two equations in the form of y = mx + c and draw two lines for them on the same grid.

 

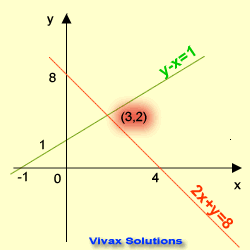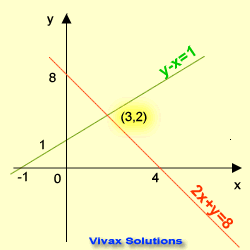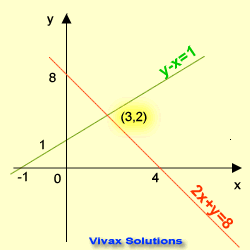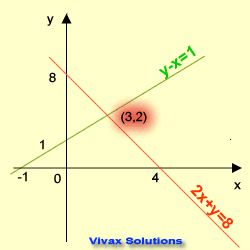
The coordinates of the point of intersection are x = 3 and y = 2.
So, the solutions are x = 3 and y = 2.

 

Simultaneous Equations Generator

With this simple programme, you can generate questions at random, along with answers - unlimited number of questions. Generate the questions first, work out the solution and then check with the answer shown below the question.

 

Simultaneous Equations - problem solving

Equations that must be solved at the same time are simultaneous equations.

E.g.1

The sum of two numbers is 6 and the difference is 2. Find the numbers.
Let the numbers be x and y.
x + y = 6 1
x - y = 2 2
1 + 2 => 2x = 8
x = 4
Sub in 1=> 4 + y = 6
y = 2
The numbers are x = 4 and y = 2.

E.g.2

The sum of two books and a pencil is £6.00. The difference of cost between 3 books and 2 pencils is £2.00. Find the cost of a book and a pencil.
Let the cost of a book be x and that of a pencil be y.
2x + y = 6 1
3x - 2y = 2 2
1 X 2 => 4x + 2y = 123
2 + 3 => 7x = 14
x = 2
Sub in 1
4 + y = 6
y = 2
The cost of a book and a pencil is £2.00 each.

E.g.3

If I double a number and add three times a second number, the answer is 1. If I multiply the first number by 3 and take away twice the second number, the answer is 8. Find the numbers.
Let the numbers be x and y.
2x + 3y = 1 1
3x - 2y = 8 2
From 1 - 3y => 2x = (1 - 3y)
x = (1 - 3y)/2
Sub in 2 => 3(1 - 3y)/2 - 2y = 8
X 2 => 3(1 - 3y) - 4y = 16
3 - 9y - 4y = 16
3 - 13y = 16
-3 => -13y = 13
y = -1
Sub in 1 => 2x - 3 = 1
+ 3 => 2x = 4
x = 2
The numbers are x = 2 and y = -1.

E.g.4

The sum of twice the cost of a box biscuits and the cost of a box chocolates is £8.00. The difference between the cost of box of chocolates and the box of biscuits is £1.00. Find the cost of each.
Let the cost of the box chocolates and the box of biscuits be y and x respectively.
2x + y = 8 1
y -x = 1 2
1 => y = 8 - 2x
Sub in 2 => y = 8 - 2x - x = 1
8 - 3x = 1
-8 => -3x = -9
:- -3 => x = 3
Sub in 1 => 6 + y = 8
-6 => y = 2
The cost of box of chocolates =£2.00 and that of biscuits = £3.00.

Solving Simultaneous Equations - fully interactive

The following applet help you solve simultaneous equations instantly. Just type in the two equations into the text boxes, exactly in the form shown, and then press enter. You may move the grid to see the point of intersection of the two lines.

 

 

Questions for Practice

Now, in order to complement what you have just learnt, work out the following questions:

1. The sum of two numbers is 18. The difference is 4. Find the numbers.
2. A straight line passes through (3 , -4) and (5 , 8). Find the equation of the line.
3. The cost of 3 DVD's and 4 CD's is £62.00. The cost of 4 DVD's and 3 CD's is £64.00. Find the cost of each.
4. A diver swims downstream a distance of 40 miles in two hours. If he swims upstream, he can only move 16 miles during the same time. Find his swimming speed and the speed of the river.
5. Half the difference between two numbers is 8. The average of the numbers is 12. Find the numbers.
6. Nicole has 23 notes of £20 and £5 in her hand bag. The amount of money she has in the bag is £340.00. Find the number of notes of each type.
7. There are two angles on a straight line. One angle is 15 more than twice the other. Find the size of each angle.
8. The sum of ages of an uncle and his nephew two years ago was 40. In two years time from now, the age of the uncle will be three times that of his nephew by then. Find their ages in 7 years time.
9. The curve, px² + qx, passes through (3,6) and (1,-2). Find the values of p and q.
10. The numerator of a fraction is 3 smaller than its denominator. If both the numerator and denominator are increased by by 1, the fraction is 5/8. Find the original fraction.
11. A car covers a distance of 220 miles at 3o mph and 20 mph respectively. Find the time taken for each part of the journey.
12. The curve, px² + qx + r, passes through (0,5) and (2,5) and (3,11). Find the values of p, q and r.

 

Answers

Move the mouse over, just below this, to see the answers:

1. 11,7
2. y = 6x - 22
3. 10,8
4. 14,6
5. 20,4
6. 15,8
7. 125, 55
8. 34, 10
9. 2, -4
10. 4/7
11. 6, 2
12. 2, -4, 5

 

Factorisation

The following examples show how to factorize algebraic expressions.

Basic Factorisation

The process of taking common factors out in an algebraic expression is called factorising

E.g.1

2x + 8
2(x + 4)

E.g.2

2x + 8y
2(x + 4y)

E.g.3

4x² + 6x
2x(2x + 3)

E.g.4

ax²p - 2ax³r
ax²(p - 2xr)

Factorising in Pairs

In this method, we pair up the terms and then factorize twice as follows:
x² + 6x + 2x + 12
x² + 6x + 6x + 12
First factorizing:
x(x + 6) + 2(x + 6)
Second factorizing:
(x + 6)(x + 2)

E.g.1

2ax + 6ay + bx + 3by
2a(x + 3y) + b(x + 3y)
(x + 3y)(2a + b)

E.g.2

xk - xl - yk + yl
x(k - l) - y(k - l)
(k - l)(x - y)

E.g.3

x² - 6x + 4x - 24
x(x - 6) + 4(x - 6)
(x - 6)(x + 4)

E.g.3

x² - 3x - 2x + 6
x(x - 3) - 2(x - 3)
(x - 3)(x - 2)

Factorizing Quadratic Expressions - easier

An expression with the highest term of x being a squared one, is called a quadratic expression.

E.g.1

x² + 6x + 8
Think of two factors of 8 that add up to 6 - 4 and 2.
Now, split up the middle term into 4x and 2x
x² + 4x + 2x + 8
Now, factorize in pairs
x² + 4x + 2x + 8
x(x + 4) + 2(x + 4)
(x + 4)(x + 2)

E.g.2

x² - 6x + 8
Think of two factors of 8 that add up to -6 - -4 and -2.
Now, split up the middle term into -4x and -2x
x² - 4x - 2x + 8
Now, factorize in pairs
x² - 4x - 2x + 8
x(x - 4) - 2(x - 4)
(x - 4)(x - 2)

E.g.3

x² + 6x - 16
Think of two factors of -16 that add up to 6 - 8 and -2.
Now, split up the middle term into 8x and -2x
x² + 8x - 2x - 16
Now, factorize in pairs
x² + 8x - 2x - 16
x(x + 8) - 2(x + 8)
(x + 8)(x - 2)

Factorizing Quadratic Expressions - harder

E.g.1

2x² + 13x + 6
Multiply 2 and 3 first - 2 x 6 = 12.
Think of two factors of 12 that add up to 13 - 12 and 1.
Now, split up the middle term into 12x and x
2x² + 12x + x + 6
Now, factorize in pairs
2x² + 12x + x + 6
2x(x + 6) + 1(x + 6)
(x + 6)(2x + 1)

E.g.2

3x² - 11x + 6
Multiply 3 and 6 first - 3 x 6 = 18.
Think of two factors of 18 that add up to -11 - -9 and -2.
Now, split up the middle term into -9x and -2x
3x² - 9x - 2x + 6
Now, factorize in pairs
3x² - 9x - 2x + 6
3x(x - 3) - 2(x - 3)
(x - 3)(3x - 2)

E.g.3

4x² - 8x - 5
Multiply 4 and 5 first - 4 x 5 = -20.
Think of two factors of 20 that add up to -8 - -10 and 2.
Now, split up the middle term into -10x and 2x
4x² - 10x + 2x - 5
Now, factorize in pairs
4x² - 10x + 2x - 5
2x(2x - 5) + 1(2x - 5)
(2x - 5)(2x + 1)

Factorizing Difference of Squares

x² - y² = (x + y)(x - y)

E.g.1

x² - 9
x² - 3²
(x + 3)(x - 3)

E.g.2

4x² - 9y²
(2x)² - (3y)²
(2x + 3y)(2x - 3y)

E.g.3

x² - 9/4
x² - (3/2)²
(x + 3/2)(x - 3/2)

E.g.4

x³ - 9x/4
x[x² - 9/4]
x[x² - (3/2)²]
x[(x + 3/2)(x - 3/2)]
x(x +3/2)(x - 3/2)

E.g.4

Find 101² - 99²
(101 - 99)(101 + 99)
2 x 200
400

Now, please practise the following:

1. 3x² - 12x
2. x² - 12x + 20
3. 2x² - 9x -5
4. x² - 25/49
5. x³ - 36x/81
6. x³ - x² + 2x - 2
7. x³ - y² - x² + xy²
8. 5x³ + 5x² - x - 1
9. ax + bx + ay + by - cx - cy
10. 12x² - 8x³ + 9 - 6x

Challenge

The sum of the two factors of x/y - y/x is x/y + y/x . Find the two factors.

 

Factorable Expression Generator

With this simple programme, you can generate questions at random, along with answers in the form of factors - unlimited number of questions. Generate the questions first, work out the solution and then check with the answer shown below the question.

Quadratic Equations

An equation in the form of ax² + bx + c = 0 is called a quadratic equation.

E.g.

• x² + 6x + 8 = 0
• 2x² - 5x + 6 = 0
• x² - 6 = 0
• x² - 6x = 0

A quadratic equation has two solutions; that means there are two values for x that satisfy the equation. There are four different ways to solve a quadratic equation:

1. Factorizing Method
2. Formula Method
3. Graphical Method
4. Completing the Square Method

Factorizing

E.g.1
x² + 8x = 0
x(x + 8) = 0
x = 0 or (x + 8) = 0
x = 0 or x = -8

E.g.2

x²= 6x
x² - 6x = 0
x(x - 6) = 0
x = 0 or (x - 6) = 0
x = 0 or x = 6

E.g.3

x² + 6x + 8 = 0
x² + 4x + 2x + 8 = 0
x(x + 4) + 2(x + 4) = 0
(x + 4)(x + 2) = 0
(x + 4) = 0 or (x + 2) = 0
x = -4 or x = -2

E.g.4

x² - 6x + 8 = 0
x² - 4x - 2x + 8 = 0
x(x - 4) - 2(x - 4) = 0
(x - 4) = 0 or (x - 2) = 0
x = 4 or x = 2<

E.g.5

x² + 6x - 16 = 0
x² + 8x - 2x - 16 = 0
x(x + 8) - 2(x + 8) = 0
(x + 8) = 0 or (x - 2) = 0
x = -8 or x = 2

E.g.6

2x² + 13x + 6 = 0
2x² + 12x + x + 6 = 0
2x(x + 6) + 1(x + 6) = 0
(x + 6) = 0 or (2x + 1) = 0
x = -6 or 2x = -1
x = -6 or x = -1/2

E.g.7

x² - 9/4 = 0
(x + 3/2)(x - 3/2) = 0
x + 3/2 = 0 or x - 3/2 = 0
x = -3/2 or x = 3/2

Formula Method

If ax² + bx + c = 0, then
x = [-b ±√(b² - 4ac) ]/ 2a

E.g.1

x² - 6x + 8 = 0
a = 1; b = -6; c = 8
x = -(-6) ±√((-6)² - 4(1)(8)) / 2(1)
x = 6 ±√(36 - 32) / 2
x = 6 ±√(4) / 2
x = (6 ± 2 )/ 2
x = 4 or x = 2

E.g.1

2x² - 5x + 3 = 0
a = 2; b = -5; c = 3
x = -(-5) ±√((-5)² - 4(2)(3)) / 2(2)
x = 5 ±√(25 - 24) / 4
x = 5 ±√(1) / 4
x = (6 ± 1 )/ 4
x = 1.5 or x = 1

 

Graphical Method

In this method, a graph is plotted for a quadratic function. The graph takes the typical shape, known as parabola.

E.g. Solve x² + 5x - 7 = 0

First of all, make a table for both x and y of the function.

x	y
-2	-13
-1	-11
0	-7
1	-1
2	7
3	17

 

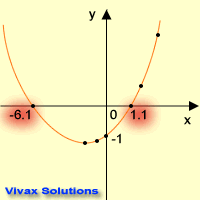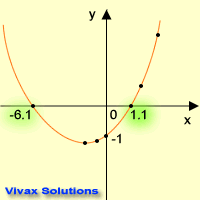
Now, plot a graph of y against x. Note the points at which the curve the crosses the x-axis. They are the solutions of the quadratic function. The solutions are:
x = 1.1 or x = -6.1

The following animation is interactive: it shows how to solve a quadratic equation by a graph; by clicking on the button, you can generate a random equation and its solutions appear at the same time. If there are no solutions - the graph being above the x-axis - instead of solutions, the word, undefined, appears in those places.

 

 

Completing the Square Method

x² + 4x - 5 = 0
Let (x + a)² + b = x² + 4x - 5
x² + 2ax + a² + b = x² + 4x - 5
Now, make the coefficients of x and the constant equal.
x => 2a = 4
a =2
a² + b = -5
4 + b = -5
b = -9
(x + 2)² - 9 = 0
(x +2)² = 9
(x + 2) = ±3
x = -2 ±3
x = 1 or -5

 

Now, in order to complement what you have just learnt, work out the following questions:

Click the button to get the quadratic equations; solve them by all four methods to master the techniques.

Quadratic Equation Generator

 

Simultaneous Quadratic Equations

These equations are simultaneous as there are two unknowns in them; since one of the unknown is in quadratic form, they are quadratic too. Therefore, these equations have two sets of solutions, one for each unknown.

E.g.1

The equation of a circle is x² + y² = 45. It intersects with, y = 2x, at two points. Find the coordinates of the points of intersection.
x² + y² = 45 1
y = 2x 2
Sub y in 1 => x² + 4x² = 45
5x² = 45
:- 5 => x² = 9
x = ± 3
Sub in 2 => y = ±6
Solutions: (3,6); (-3,-6)

E.g.2

The equation of a circle is x² + y² = 25. It intersects with the line, x + y = 7, at two points. Find the coordinates of the points of intersection.
x² + y² = 25 1
x + y = 7 2
y = (7-x)
Sub y in 1 => x² + (7-x)² = 25
x² 49 - 14x + x² = 25
2x² - 14x + 24 = 0
x² - 7x + 12 = 0
(x - 4)(x - 3) = 0
x = 4 or x = 3
Sub in 2
y = 3 or y =4
Solutions: (4,3); (3,4)

 

Simultaneous Quadratic Equation Generator

With this simple programme, you can generate questions at random, along with answers - unlimited number of questions. Generate the questions first, work out the solution and then check with the answer shown below the question. If you don't see the solutions, please click the refresh button on the applet once.

 

Quadratic Equations - word problems

You will get an amazing set of worked examples here involving quadratic equations. In addition, there are lots of questions for you to practise in order to complement your experience that you get from these examples.

E.g.1

The sum of two numbers is 27 and their product is 50. Find the numbers.
Let one number be x. Then the other number is 50/x.
x + 50/x = 27
X x => x² + 50 = 27x
- 27x => x² - 27x + 50 = 0
(x -25)(x -2) = 0
(x -25) = 0 or (x -2) = 0
x = 25 or x = 2.

E.g.2

The length of a rectangle is 5 cm more than its width and the area is 50cm². Find the length, width and the perimeter.
Let the width be x. Then the length = x + 5.
x(x + 5) = 50
x² + 5x = 50
-50 => x² + 5x - 50 = 0
(x + 10)(x -5) =0
(x + 10) = 0 or (x -5) =0
x = -10 or x = 5 - x = -10 is impossible to be a width
Width = 5cm; so, the length = 10cm.
Perimeter = 30cm.

E.g.3

The three sides of a right-angled triangle are x, x+1 and 5. Find x and the area, if the longest side is 5.
The hypotenuse = 5
x² + (x+1)² = 5² (Pythagoras' Theorem)
x² + x² + 2x + 1 = 25
-25 => x² + x² + 2x - 24 = 0
2x² + 2x - 24 = 0
x² + x - 12 = 0
(x - 3)(x + 4) = 0
(x + 4) = 0 or (x - 3) = 0
x = -4 or x = 3
x = 3;
Area = 1/2 x 3 x 4 = 6cm²

E.g.4

The product of two numbers is 24 and the mean is 5. Find the numbers.
Let one number = x; then the other = 24/x
(x + 24/x)/2 = 5
X 2 => x + 24/x = 10
X x => x² + 24 = 10x
- 10x => x² + -10x + 24 = 0
(x - 6)(x -4) = 0
(x - 6) = 0 or (x -4) = 0
x = 6 or x =4
The numbers are 6 or 4.

E.g.5

The sum of numbers is 9. The squares of the numbers is 41. Find the numbers.
These are quadratic simultaneous equations.
let the numbers be x and y.
x + y = 9
x² + y² = 41
From the first equation, y = (9-x)
Now substitute this in the second equation.
x² + (9-x)² = 41
x² + 81 - 18x + x² = 41
2x² - 16x + 81 = 41
2x² - 16x + 40 = 0
x² - 8x + 20 = 0
(x - 5)(x -4) =0
(x - 5) = 0 or (x -4) =0
x = 5 or x = 4
Substitute in the first equation, y = 5 or 4
The numbers are 5 and 4.

 

Mathematical Modelling with Quadratic Functions

There are quite a few real life situations that can be modelled by a quadratic function in an accurate way. For instance, the motion of a ball, thrown upwards to move under gravity, can be easily modelled by a quadratic equation. Using the model, we can calculate the height of the ball if the time is known or vice versa.

 

E.g.6

A ball is thrown upwards from a rooftop, 80m above the ground. It will reach a maximum vertical height and then fall back to the ground. The height of the ball from the ground at time t is h, which is given by,
h = -16t² + 64t + 80.

1. What is the height reached by the ball after 1 second?
2. What is the maximum height reached by the ball?
3. How long will it take before hitting the ground?

Follow the graph along with the calculation for a better understanding:

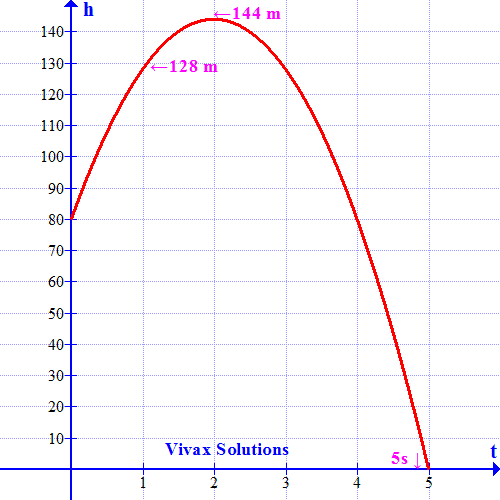
1) h = -16t² + 64t + 80
h = -16* 1*1 + 64*1 + 80 = 128m
2) Rearrange by the completing the square, we get:
h = -16[t² - 4t - 5]
h = -16[(t - 2)² - 9]
h = -16(t - 2)² + 144
When the height is maximum, t = 2; therefore, maximum height = 144m.
3) When the ball hits the ground, h = 0;
-16t² + 64t + 80 = 0
Divide the equation by -16
t² - 4t - 5 = 0
(t - 5)(t + 1) = 0
t = 5 or t = -1
The time cannot be negative; so, the time = 5 seconds.

 

E.g.7

A farmer wants to make a rectangular pen for his sheep. He has 60m fencing material to cover three sides with the other side being a brick wall. How should he use the fencing material to maximize the space for his sheep? How should he choose length and width of the pen to achieve his objective?

He just has to cover three sides; let the width be x.
Then the length = (60-2x)
Area of the pen = x(60-2x)
= 60x -2x²
Now let's sketch a graph for the quadratic equation. Which is as follows:

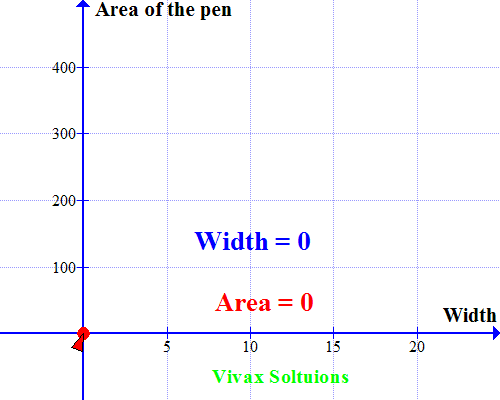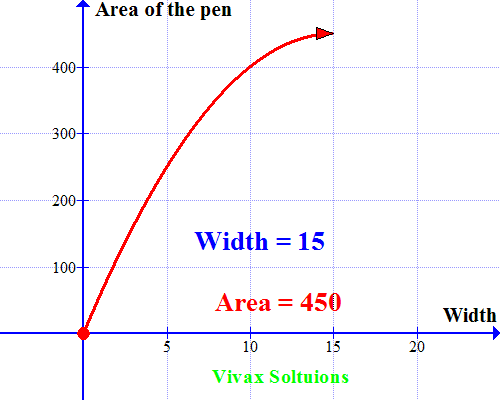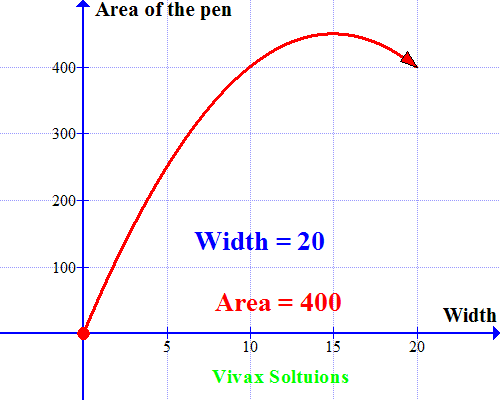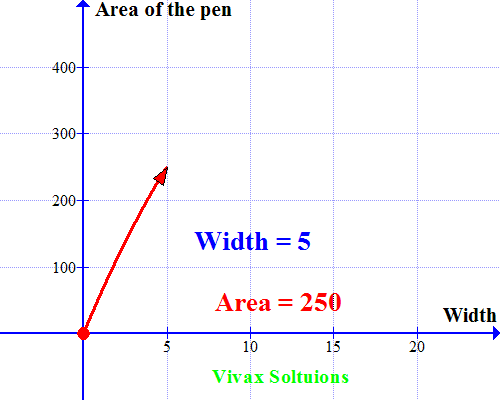
As you can see, the curve peaks at x = 15; when the width = 15m, the area is maximum. A very useful way to use quadratic equations in real life, indeed!

 

E.g.8

Two resistors, when connected in series, have a total resistance of 25 Ohms. If they are connected in parallel, the value goes down to 6 Ohms. Find the values.

When they are in series, if one resistor is x, then the other is 25-x
When they are in parallel, 1/6 = 1/x + 1/(25-x)
1/6 = 25/[x(25-x)] = 25/[25x - x²]
25x - x² = 150
If ax² + bx + c = 0, then
x = [-b ±√(b² - 4ac) ]/ 2a
x² - 25x + 150 = 0
a = 1; b = -25; c = 150
x = -(-25) ±√((-25)² - 4(1)(150)) / 2(1)
x = 25 ±√(625 - 600) / 2
x = 25 ±√(25) / 2
x = (25 ± 5 )/ 2
x = 15 or x = 10
So, the resistors are 15 Ohms or 10 Ohms.

 

 

E.g.9

The following picture shows the shape of a certain grass patch. If the area of the patch is 80m², find k.

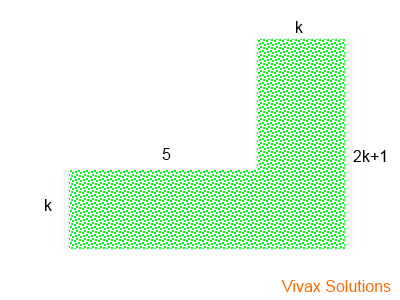
The total area = 5k + k(2k+1)
= 5k + 2k² + k
= 2k² + 6k
Since the area is 80m²
2k² + 6k = 80
2k² + 6k - 80 = 0
(2k - 10)(k + 8) = 0
k = 5 or k = -8
Since the length cannot be negative, k = 5.

 

E.g.10

The following picture shows the shape of a rectangle from which a smaller rectangular part is removed. If the remaining area of the larger rectangle is 35cm², find k.

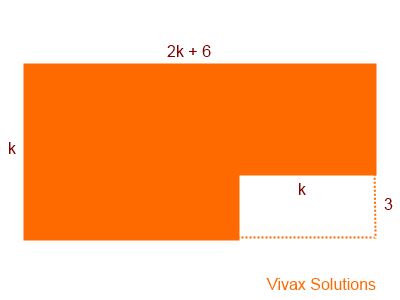
The remaining area = k(2k+6) - 3k
= 2k² + 6k -3k
= 2k² + 3k
Since the area is 35cm²
2k² + 3k = 35
2k² + 3k - 35 = 0
(2k -7)(k + 5) = 0
k = 3.5 or k = -5
Since the length cannot be negative, k = 3.5.

 

E.g.11

The shortest side of a right-angled triangle is 6cm shorter than its hypotenuse. The difference in length of other two sides is 3cm. If the shortest side is n-3, show that 2n² = 12n. Hence, find n.

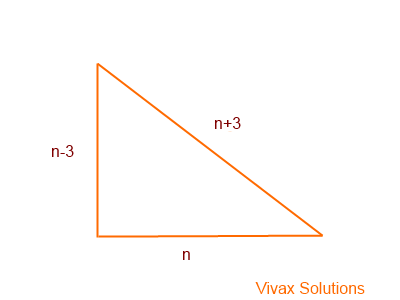
If the length of the shortest side is n-3, the length of the hypotenuse and the other side are n+3 and n respectively.
So, using Pythagoras Theorem,
(n-3)² + n² = (n+3)²
n² - 6n + 9 + n² = n² + 6n + 9
n² = 12n
n² - 12n = 0
n(n - 12) = 0
n = 0 or n = 12.
Since the length cannot be zero, n = 12.

 

E.g.12

Two cyclists move away from a town along two perpendicular paths at 20 mph and 40 mph respectively. The second cyclist starts the journey an hour later than the first one. Find the time taken for them to be 100 miles apart.

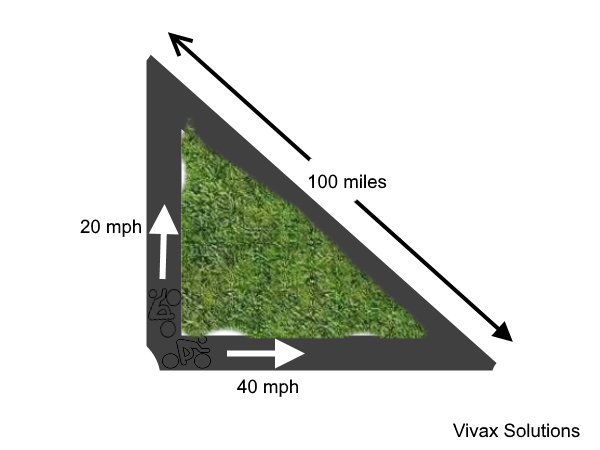
Suppose the time taken by the first cyclist is t; then the time taken by the other cyclist = (t-1)
The distances travelled by them are 20t and 40(t-1) respectively.
Using Pythagoras Theorem,
(20t)² + [40(t-1)]² = 100²
400t² + 1600(t-1)² = 10000
t² + 4t² - 8t + 4 = 25
5t² - 8t -21 = 0
(5t + 7)(t -3) = 0
t = 3 or t = -1.4
Since time cannot be negative, t = 3hrs.

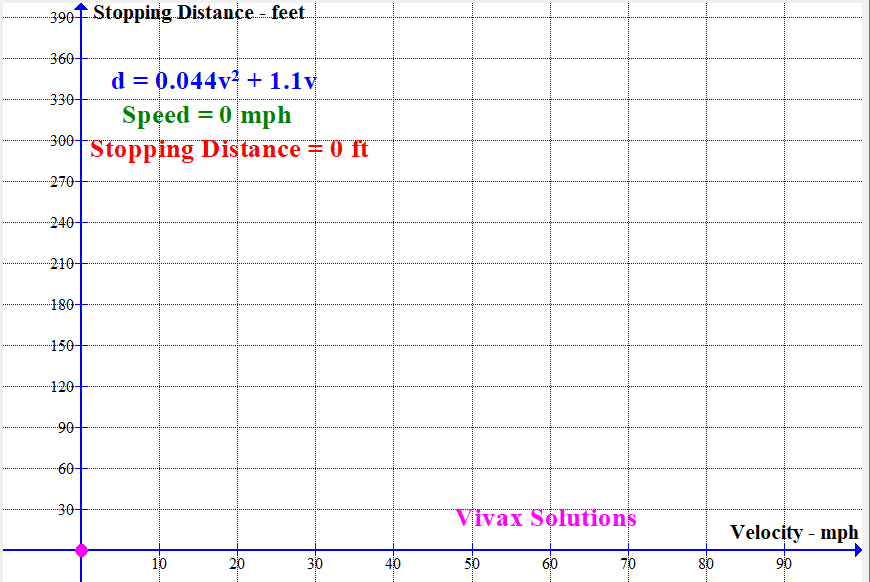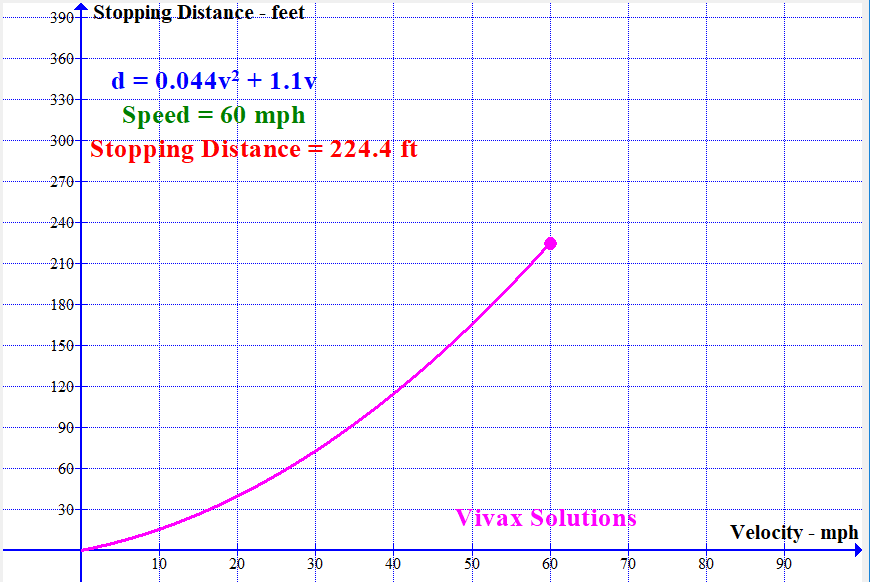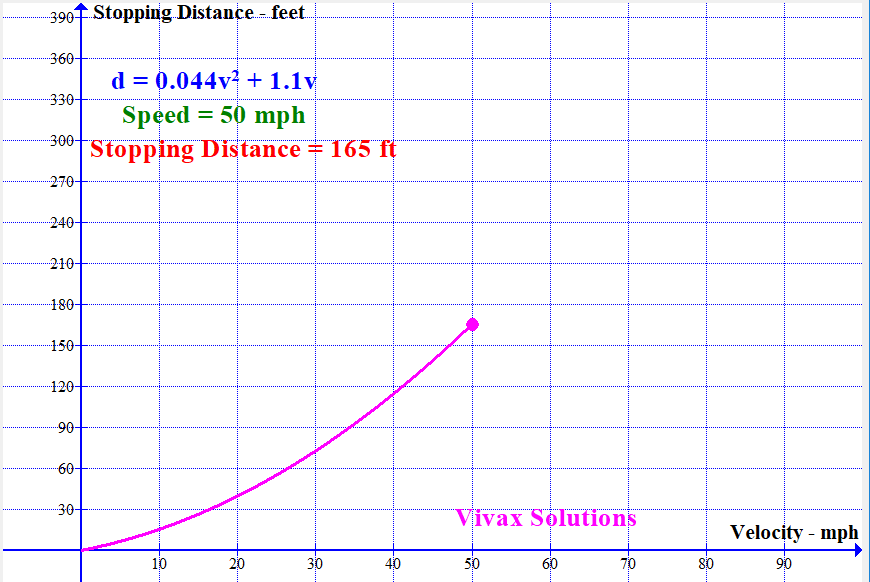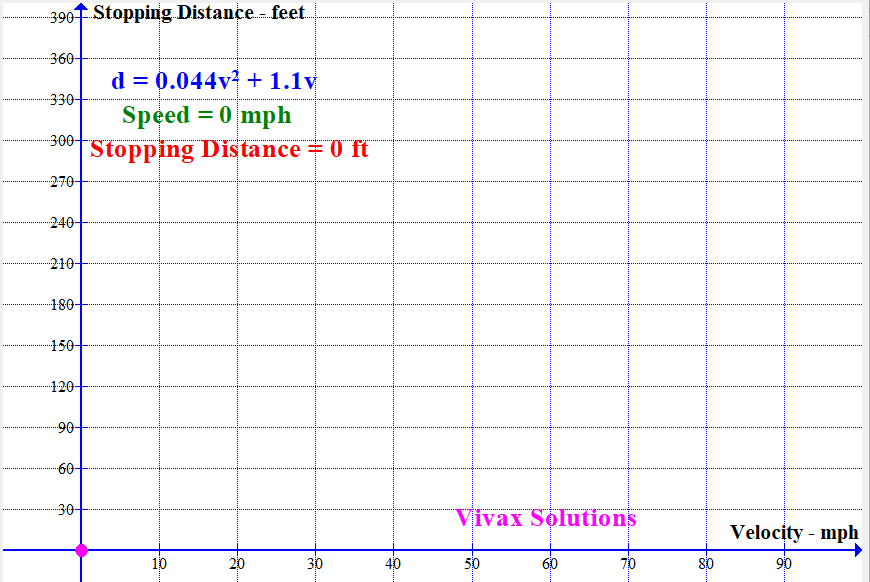
Modelling Stopping Distance of a Vehicle with Speed

With the available data, the stopping distance - sum of thinking distance and breaking distance - can be modelled by a quadratic function. It is as follows:

 

Stopping Distance
Thinking Distance	Breaking Distance

 

If the stopping distance = d and the speed = v,
d = 0.044v² + 1.1v

The following animation shows how the stopping distance, modelled by the above equation, changes with the speed:

 

 

 

Infinite Square Root Problem

Solve the following infinite square root problem:

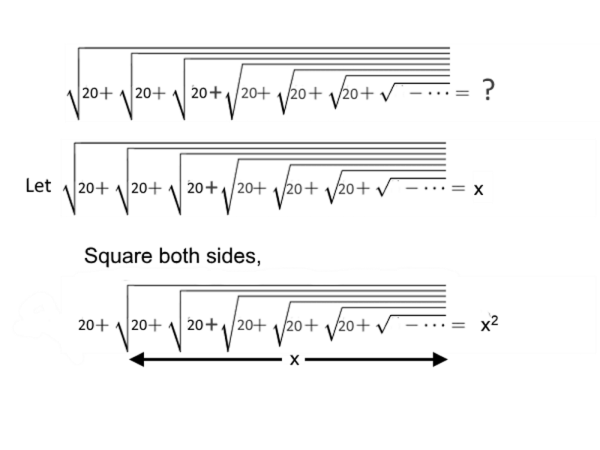
20 + x = x²
x² - x - 20 = 0
x = (1 ± √1 + 80)/2
x = (1 ± √81)/2
x = (1 ± 9)/2
x = 5 or x = -4
Since the square root of a negative number cannot be found, x = 5. So, the value of the above infinite square problem is 5.

 

Now, in order to complement what you have just learnt, work out the following questions:

Questions

1. The sum of squares of two consecutive even numbers is 244. Find the numbers.
2. The base length of a triangle is 2cm more than its height. The area is 24cm². Find the length of hypotenuse and the perimeter of the triangle.
3. The length of a square is increased by a 5^th so that its new area is 44cm² more than the original value. Find the difference in perimeter of two shapes.
4. The length and width of a rectangular garden are 150m and 120m. A foot path of regular width is added to the boundary of the garden and the total area of the garden becomes 2800m² more than its original area. Find the width of the footpath.
5. Adam is about to embark on a journey on a narrow country lane that covers 32km and decides to go at x km/h. On second thoughts, he calculates that if he increases the speed by 4km/h, his journey time can be cut down by 4 hrs. Find x.
6. The reciprocal of the sum of reciprocals of two numbers is 6. The sum of numbers is 25. Find the numbers.
7. The speed of an ant is (2t + 10) and after travelling for t minutes, it covers a distance of 12m. Find t.
8. Two chords and a diameter form a triangle inside a circle. The radius is 5cm and one chord is 2cm longer than the other one. Find the perimeter and the area of the triangle.
9. The sum of a number and it reciprocal is 26/5. Find the number.
10. The product of two numbers is 20. The sum of squares is 41. Find the numbers.
11. The dimensions of the glass plate of a wedding photo are 18cm and 12cm respectively. A new frame of equal width is about to be fitted around the glass so that the area of the frame is the same as that of the glass. Find the width of the frame.
12. A group of acquaints went to a restaurants for a meal. When the bill for £175 was brought by a waiter, two of the cheeky ones from the group just sneaked off before the bill was paid, which resulted in the payment of extra £10 by each remaining individual. How many were in the group at first?
13. Ashwin and Donald decided to set out from two towns on their bikes, which are 247 miles apart, connected by a straight t Roman road in England. When they finally met up somewhere between the two towns, Ashwin had been cycling for 9 miles a day. The number of days for the whole adventure is 3 more than the number of miles that Donald had been cycling in a day. How many miles did each cycle?
14. When a two-digit number is divided by the product of the two digits, the answer is 2 and if 27 is added to the number, the original number turns into a new number with the digits being swapped around. Find the number.
15. There are three numbers: the difference of the differences of them is 5. The sum and product are 44 and 1950 respectively. Find the numbers.
16. Find the two numbers, whose sum is 19 and the product of the difference and the greater, is 60.
17. A boy was asked his age: "If you add the square root of it to half of it, and then subtract 12, the answer will be nothing," replied the boy. What was his age?
18. A group of army cadets, consisting of 1066 men, form two squares in front of a garrison. In the side of one square, there are 4 more men than the other. How many men are in each side of the squares?
19. The height of a triangle is 4cm less than three times its base length. If the area is 80 cm², find the lengths of the base and height.
20. An isosceles triangle is inscribed in a circle in such a way that its longest side, which goes through the centre is √50cm. Find the area of the triangle.
21. A butcher bought some pheasants for £100.00. Had each cost £1 less, he would have bought 5 more. How many pheasants did he buy?
22. The sum of reciprocals of two consecutive integers is 13/42. Find the integers.
23. The product of two numbers and the difference between them are 289 and 20 respectively. Find the numbers.
24. The sum of two numbers is 20. The sum of squares is 250. Find the numbers.
25. The area of a square exceeds twice that of another by 56cm². If the difference of the perimeter between the two is 24cm, find the area of the smaller square.

 

Answers

Move the mouse over, just below this, to see the answers:

1. 10, 12
2. 10cm, 24cm
3. 8cm
4. 5m
5. 4km/h
6. 10, 15
7. 1
8. 24cm, 24cm²
9. 5
10. 5 and 4
11. 3cm
12. 7
13. 117 and 130 miles
14. 36
15. 6, 13, 25
16. 12,7
17. 16
18. 21 and 25
19. 8cm, 20cm
20. 12.5cm²
21. 20
22. 6, 7
23. 27, 7
24. 15, 5
25. 100 or 4

 

Direct and Inverse Variation/Proportion

There are a few worked examples of the topic, shown below. In addition, there are a few questions for you to practise.

Direct Variation

When one quantity increases, if another quantity increases with that, it is called direct variation.
E.g.
The length of a rubber band (l) and the force that stretches it (F), are in direct variation.
l ∝ F
l = kF, where k is a constant.

Please move the slider and experiment with it.

l ∝ F

E.g.3

The length of a rubber band, when stretched by 20N is 6cm. Find the length, when the force is raised to 60N. Find the Force that keeps the length at 15cm.
l ∝ F
l = kF
When l = 6 and F = 20,
6 = k x 20
k = 6/20
When F = 60,
l = 6/20 x 60 = 18
F = 18 N.
When l = 15,
15 = 6/20 x F
F = 50N.

E.g.4

The power of a certain device (P) is directly proportional to the square of the current through it. The power is 60W, when the current is 2Amps. Find the power, when the current is 3Amps. Find the current when the power is 90W.
P ∝ I²
P = k I²
When I = 2 and P = 60,
60 = K X 4
k = 15
When I = 3,
P = 15 x 9
P = 135W.
When P = 90,
90 = 15 * I²
I = 2.3A.

Inverse Variation

When one quantity increases, if another quantity decreases with that, it is called inverse variation.
The volume of a fixed mass of gas is inversely proportional to the pressure.
V ∝ 1/P
V = k1/P

Please move the slider and experiment with it.

P ∝ 1 / V

E.g.5

The volume of a gas container is 3cm³ when pressure is 12Pa. Find the volume, when the pressure is 36N. At what pressure, will the volume be 9cm³?
When P = 12 and V = 3,
3 = k x 1/12
k = 36
When P = 36,
V = 36 x 1/36 = 1
V = 1cm³
When v = 9,
9 = 36 x 1/P
P = 4Pa.

E.g.6

The force between two magnets is inversely proportional to the distance between them. When the distance is 3cm, the force is 12N. Find the force, when the distance is 2cm. Calculate the distance, when the force is 432N as well.
F ∝ 1/d²
F = k 1/d²
When d = 3 and F = 12,
12 = k x 1/9
k = 108
When d = 2,
F = 108 x 1/4
F = 27N.
When F = 432,
432 = 108 x 1/d²
d² = 1/4
d = 1/2cm.

Now, in order to complement what you have just learnt, work out the following questions:

1. The distance d through which a feather falls from rest is proportional to the square of the time taken t. if the feather falls 15m in 3 seconds, how far will it fall in 9 seconds? How long will it take to fall 45m?
2. The energy E stored in a square-plated capacitor varies as the square of the length of the side x. When the length is 3cm, the energy stored is 81 Joules. What is the energy stored when the length is 5cm? What is the length when the stored energy is 243Joules?
3. The length L of an embryo of a certain mammal is proportional to the square root of the number of hours left before its birth. If the embryo is 12 cm long before 2 hours, how long will it be after 8 hours? How long will it take to grow to a length of 18cm?
4. p is directly proportional to q. Fill in the banks.
   

   p	q
   x	60
   4	12
   1/3	y

5. L is directly proportional to (M - 2). L is 36 when M is 4. Find L when M = 10. Find M when L = 108.
6. The kinetic energy of an object is proportional to the square of its speed. The kinetic energy is 64J when the speed is 4m/s. Find the kinetic energy when the speed is 20m/s. At which speed will the Kinetic energy be 900J?
7. The frictional force against the motion of a car is proportional to the square of the speed of the car. If this force is 16000N at 10 m/s, what is the force at 30 m/s? At what speed is the force equal to 900N?
8. The force of attraction between any two stars is inversely proportional to the square of the distance between them. The force between two, when they are 4 light years apart is 24x10⁶⁴N.Find the force when the distance is 3 light years. If the force is 48x10⁶⁴N, find the distance between them too.
9. In the following table, p is inversely proportional to q. Fill in the blanks.
   

   p	q
   x	60
   4	3
   1/3	y

10. y is inversely proportional to (x - 3). y = 4 when x = 5. Find y when x = 18. Find x when y = 144.

 

Algebraic Proofs

These worked example mainly focus on the proof involving even and odd numbers that often appear in GCSE/iGCSE examination papers.

In this chapter, an even number is denoted as 2n and an odd number as 2n + 1, where n is an integer.

E.g.1

Show that the sum of squares of two consecutive odd numbers is a multiple of 4 added to 2.
Let the numbers be (2n + 1) and (2n + 3).
(2n + 1)² + (2n + 3)² = 4n² + 4n + 1 + 4n² + 12n + 9
8n² + 16n + 10 = 4[n² + 4n + 2] + 2

E.g.2

Show that the sum of squares of two consecutive even numbers is a multiple of 4.
Let the numbers be (2n) and (2n + 2).
(2n)² + (2n + 2)² = 4n² + 4n² + 8n + 4
8n² + 8n + 4 = 4[2n² + 2n + 1]

E.g.3

Show that the difference of squares of two consecutive numbers is always an odd number.
Let the numbers be x and (x + 1).
(x + 1)² - x² = x² + 2x + 1 - x²
= 2x + 1, an odd number regardless of x.

E.g.4

Show that the difference of squares of two consecutive odd numbers is a multiple of 8.
Let the numbers be (2n + 1) and (2n + 3).
(2n + 3)² - (2n + 1)² = 4n² + 12n + 9 - 4n² - 4n - 1
8n² + 8n + 8 = 8[n² + n + 1]

E.g.5

Show that the expression, x² - 6x + 11, is always positive regardless of x.
By completing the square, x² - 6x + 11 = (x - 3)² + 2
Since, being a square, (x - 3)² is always positive, so is (x - 3)² + 2.

E.g.6

Show that the sum of four consecutive integers is always even.
Let the numbers be x, x + 1, x + 2 and x + 3
The sum = x + x + 1 + x + 2 + x + 3 = 4x + 6 = 2(2x + 3), an even number.