DeMorgan' Laws
E.g.1
De Morgan's laws are indispensable in digital electronics. The laws outlined by him are simple to understand, yet transformed the Boolean algebra in
a dramatic way.
First Law
A + B = A.B
Proof:
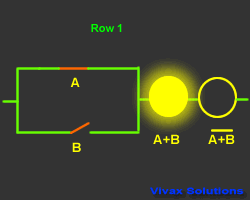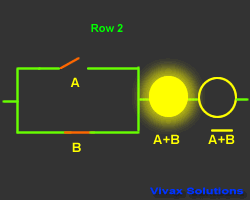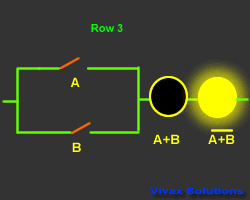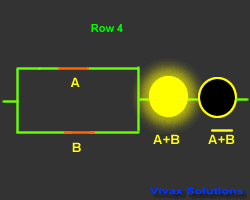
| Input and Output |
|---|
| A | B | A+B | A + B |
| 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
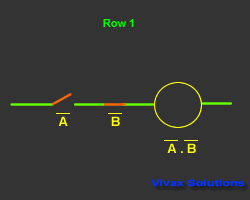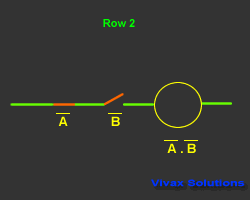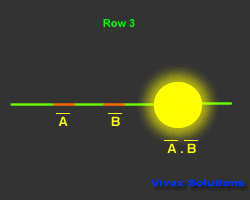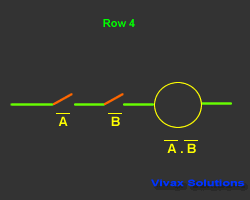
| Input and Output |
|---|
| A | B | A | B | A.B |
| 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
Second Law
A.B = A + B
Proof:
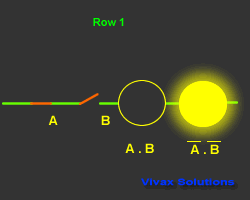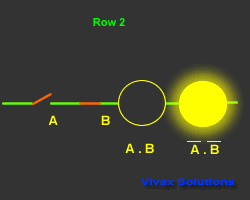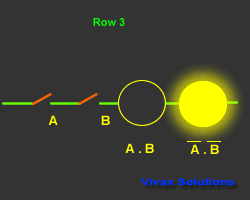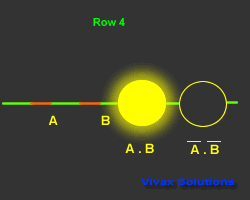
| Input and Output |
| A | B | A.B | A.B |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
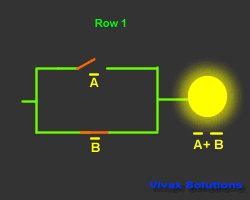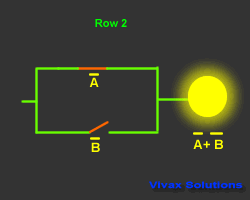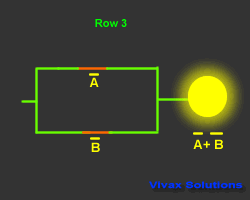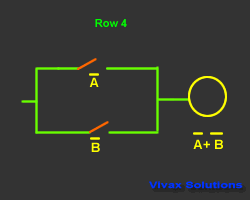
| Input and Output |
| A | B | A | B | A + B |
| 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
Now try the following with a circuit and a truth
table:
- A + B.C = A.B.C
- A + B.C + A.B = A.B
- A + AB = A + B
- AB + AB = A