Boyle's Law

Ever wondered why a balloon expands when you blow air into it or why a scuba diver's lungs compress as they dive deeper? The answer lies in Boyle's Law, a fundamental principle in physics that explains the relationship between the pressure and volume of a gas.

In this tutorial, we'll delve into the world of gases and explore how Boyle's Law works. We'll break down the complex concepts into easy-to-understand explanations, complete with real-world examples and practical applications. Whether you're a student, a curious mind, or simply looking to expand your knowledge, this guide will equip you with a solid understanding of Boyle's Law. Let's get started!

The volume of a fixed mass of gas is inversely proportional to its pressure at constant temperature.

p ∝ 1 / v
p = k 1 /v
pv = k

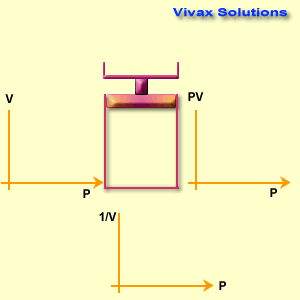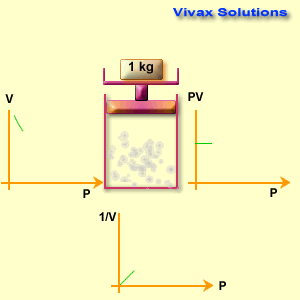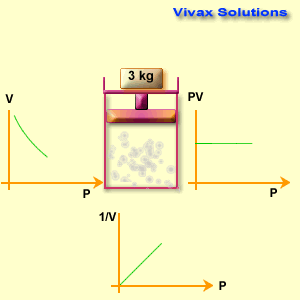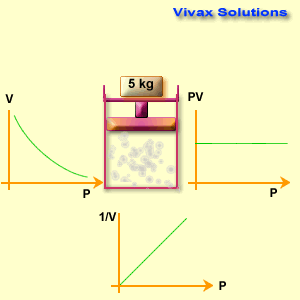
Please move the slider and experiment with it.

P ∝ 1 / V

If the pressure and volume of a fixed mass of gas take the values of p₁ v₁and p₂ v₂ respectively,

p₁ v₁ = p₂ v₂

 

E.g.1

The pressure of a fixed mass of air is 20 Pa and volume is 8 cm³. Its pressure is doubled while keeping the temperature constant. Find the volume.
p₁ = 20, v₁ = 8, p₂ = 40
According to Boyle's law,
p₁v₁ = p₂v₂
20 x 8 = v₂ x 40
v₂ = 4cm³

E.g.2

A scuba diver's tank contains 12 liters of air at a pressure of 200 atmospheres. What volume will this air occupy at the surface pressure of 1 atmosphere?
Using Boyle's Law, p₁v₁ = p₂v₂.
Plugging in the values, we get: 200 x 12 = 1 x V₂.
Solving for V₂, we find that the new volume is 2400 liters.

E.g.3

A syringe contains 5 mL of air at atmospheric pressure. The plunger is pushed in until the volume is reduced to 2 mL. What is the new pressure in the syringe?
Using Boyle's Law, p₁v₁ = p₂v₂.
Assuming atmospheric pressure is 1 atm, we get: 1 x 5 = P₂ x 2.
Solving for P₂, we find that the new pressure is 2.5 atmospheres.

E.g.4

A syringe contains 5 mL of air at atmospheric pressure. The plunger is pushed in until the volume is reduced to 2 mL. What is the new pressure in the syringe?
Using Boyle's Law, p₁v₁ = p₂v₂.
Assuming atmospheric pressure is 1 atm, we get: 1 * 5 = P₂ x 2 .
Solving for P₂, we find that the new pressure is 2.5 atmospheres.

E.g.5

A closed cylinder whose volume V, = 2.0 1 contains air at a pressure p, = 0.53 x 10⁵Pa at 20°C. Then, the cylinder is submerged in water, having the same temperature and at a depth h = 1.2 m is opened. What volume of water enters the cylinder if the atmospheric pressure at this moment is 0.99 x 10⁵Pa?
Using Boyle's Law, p₁v₁ = p₂v₂.
Assuming atmospheric pressure is 1 atm, we get: 1 * 5 = P₂ x 2.
Solving for P₂, we find that the new pressure is 2.5 atmospheres.
Using Boyle's law, p₁V₁, = p₂V₂ , where p₂ is the pressure in water at the depth h = 1.2 m, p2= 1.10 x 10⁵Pa.
Therefore, V_water= V, — V2 = V, - p,V,/p2= V,(1 — p1 /p2)= 1.045 dm3.

 

 

The following animation shows how the lungs function, following Boyle's Law.

 

 

A Quiz on Boyle's Law

 

Please answer the following questions.

1. An air column is trapped inside a capillary tube by a drop of mercury. The tube is placed horizontally and the position of the mercury drop is noted. Then the tube is raised vertically with the open end being at the top. What will happen to the mercury column? - go up or down.
2. When a coke bottle is opened, air bubbles go up from the bottom. Explain this.
3. A balloon filled with air is brought down in a lake; the deeper it goes, the more it tends to go up. Explain.
4. A 1.5 litre can is filled with nitrogen at a pressure of 8 atmospheres. What size can would be required to hold the same gas at a pressure of 4.0 atmospheres?.
5. Can you apply Boyle's law when a car tire is being filled up?. Explain you answer.
6. Two identical containers of volume 6cm³ contain the same gas at pressure 20 Pa and 12 Pa. They are linked by a valve-tube. When the valve is opened, find the resultant pressure of the system.
7. An air column has been trapped in a tube sealed at one end by a mercury column, having a height, h = 19 cm. When the tube is placed with its open end downwards, the height of the air column is, 1, = 10 cm. If the tube is turned so that its open end is at the top, the height of the air column is / 2 = 6 cm. Find the atmospheric pressure.