Electromagnetic Induction
Faraday's Discovery

Michael Faraday was one of the most eminent
pragmatic physicists we ever had. He was a self-taught gentleman, who used to love to
keep a low profile, despite the magnificent service he rendered to mankind with tireless
work.
He was never after fame or money and propelled to work by sheer enthusiasm
and clear vision.
The discovery of electricity by electromagnetic
induction was his greatest achievement. Although, it was a chance-discovery, he
had been working on the project for a long time- the chance favoured the
prepared mind, as Louise Pasteur once said.
Faraday noticed that a change in magnetic field
- flux - around a closed circuit led to the creation of an electric current in
the latter, almost out of the blue. He also noticed that the mere presence of
magnetic field does not cause any such event. So, Faraday discovered a new
phenomenon and was called Electromagnetic
Induction.
When there is a change in magnetic field in a
circuit, a voltage / current is induced in the circuit. This is called
electromagnetic induction.
The following animation shows
that:
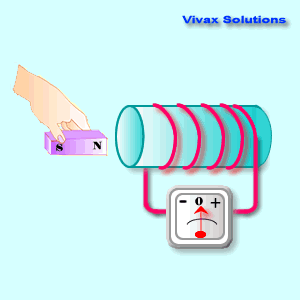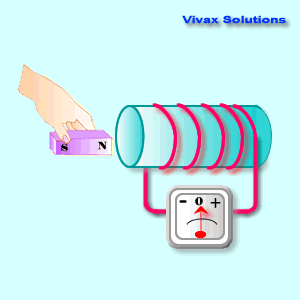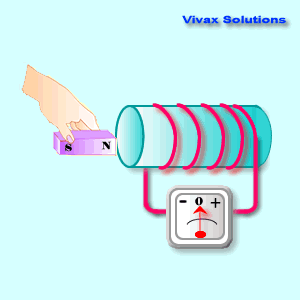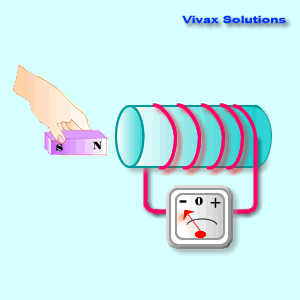
As you can see, the device shows a
current only as long as the magnet is on the move; when the magnet is static,
its reading is zero. However, there is a magnetic field around the coil. So, the
presence or absence of a magnetic field around a coil, does not induce an
electric current.
On the other hand, when the coil
moves, there is a changing magnetic field around the coil; so electromagnetic
induction takes place and the galvanometer indicates its presence in the
circuit.
We can now conclude that the
electromagnetic induction is caused by a changing magnetic field in a
circuit.
The Laws of Electromagnetic Induction
Faraday's Law
The magnitude of the induced electric voltage is directly proportional to
the rate of change of magnetic flux in the circuit.
In the following animation, move the magnet into the coil and away from it, in order to see Faraday's Law in action.
If φ is the magnetic flux, then according to Faraday's Law,
E = -dφ/dt
Click the play button to animate: the olive line is the magnetic flux; the red line represents the induced EMF.
Lenz's Law
The induced electric current goes in such a way that it produces
magnetic flux in the opposite direction to the same thing that caused in the
first place.
E.g.
There is a horizontal magnetic field of flux density B,in a certain region. A rod of length l falls vertically down this region while staying horizontal at a constant speed v. Find an expression for the induced Emf.
Discuss the direction of the induced current using Lenz's law.
If the length goes down in time t,
The distance travelled = vt
Area covered = lvt
Magnetic flux passed through = Blvt
The rate of change of magnetic flux = Blvt / t = Blv
According to Faraday's law, This is induced Emf.
E = Blv
According to Lenz's law, the induced current flows in such a way that the magnetic field exerts a force on it upwards. So, the work done in overcoming this force turns into the electrical energy that keeps
the induced current flowing. So, electromagnetic induction is compatible with the conservation of energy, although it appears to be otherwise.
Do you want to experiment with generators and motors? Then you meant electromagnetic induction and motor effect. This is the answer:


Please answer the following questions.
- A magnet is moved in front of a solenoid - to and fro. Explain how the electric energy flows through the solenoid, despite not being in contact with each other, using the laws of electromagnetic induction.
- You are provided with two solenoids, an ammeter, a battery and a switch. Design an experiment to show electromagnetic induction in one solenoid, using the other.
- Discuss the ways to increase the strength of the induced electromagnetic induction.
- How does the electromagnetic induction play the key role in transformers. Why do they not work on DC?
- A rod of length l is rotated at a speed v around one of its ends across a magnetic field of flux density B. Find an expression for the induced Emf