Simple Harmonic Motion

 

In this tutorial, you will learn:

 

Definition of Simple Harmonic Motion - SHM

If a body moves in such a way that its acceleration is directed towards a fixed point in its path and directly proportional to the distance from that point, the movement of the object is said to be simple harmonic.

The fixed point is the equilibrium position of the object in question; that is the point where the object comes to a halt at, when it loses all its energy.

a = -kx, where a and x are acceleration and the displacement respectively; k is a positive constant.

k = ω², where ω is the angular velocity(frequency).

The movement of an object in a circular path, as the following image illustrates, mimics the SHM.

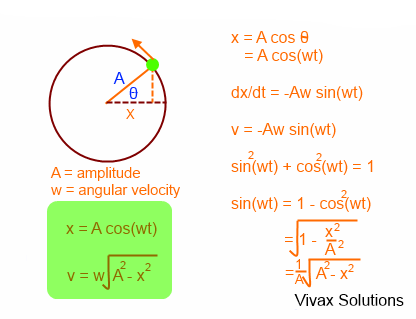
Simple Pendulum

When a simple pendulum swings to and fro, the acceleration of its bob is directed towards the centre point of its motion and is proportional to the distance from that point. Therefore, the motion of a simple pendulum is SHM.

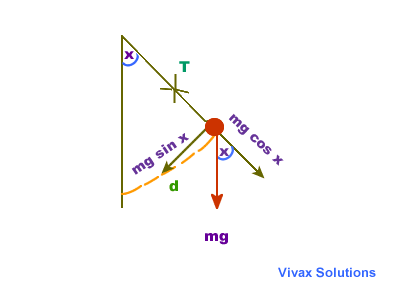
As you can see, when the weight of the pendulum bob is resolved, the tension of the string, T, and the mg cos x cancel each other out, leaving mg sin x as the net force, as shown above. This force is responsible for bringing the bob down in a curved path.
Using F = ma for the bob,
mg sin x = ma, where a is the acceleration of the bob.
If the pendulum swings through a small angle and is measured in radians, sin x is almost equal to x.
mg. x = m a
gx = a
g d/l = a ( x = d / l radians)
a = (g/l) d
a = k d
a α d
The acceleration of the bob is directly proportional to the distance from the centre point. Therefore, the motion of a simple pendulum is simple harmonic.
k = ω² where ω is the angular speed.
a = ω² d
ω² = g/l
ω = √g/l
If the time period is T,
T = 2π/ω

T = 2π √l/g

So, the time period of a simple pendulum depends only on its length; it does not depend on the mass of the bob. The formula only works for the oscillations through small angles, as it was something we assumed in the process of proof.

 

You can see the importance of the angle between the string and the vertical line being very small in the following animation.

 

 

 

A Body Attached to a Horizontal Spring

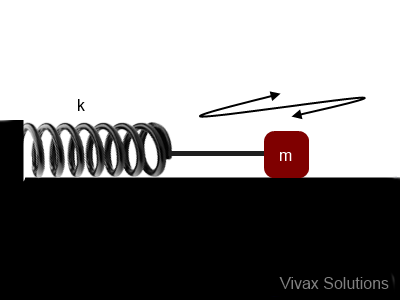
If the spring constant and the extension are k and x respectively,
Force by the spring on the object = kx
F = ma
kx = ma => a = k/m x
a ∝ x
Therefore, the motion is SHM.
So, ω² = k/m
T = 2π/ω
T = 2π √(m/k)

T = 2π √(m/k)

 

A Body Attached to a Vertical Spring

Imagine a body attached to a spring. The mass of the body and the spring constant are m and k respectively.

If the spring stretches out by e, the extension, T = ke, where T is the Tension of the spring.

Since the system is still in balance in the stage two, T = mg. Suppose the string is pulled downwards by x and then released so that it oscillates.

 

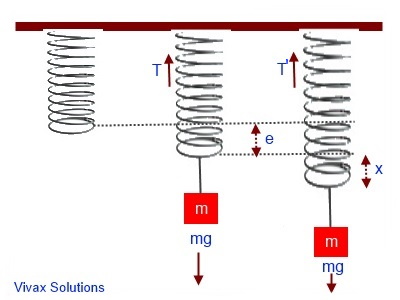
Upward force, T', when the stretched spring is released = k(e+x)
If the resultant force is F,
F = K(e+x) -mg
F = ma - Newton's Second Law
k(e+x) - mg = ma, where a is the acceleration
(ke + kx) - mg = ma
Since T = ke
mg - mg + kx = ma
ma = kx
a = k/m x
a ∝ x

ω² = k/m

T =2π √(m/k)

T =2π √(m/k)

Since the acceleration is directly proportional to the displacement , the motion is SHM.

the greater the spring constant(K), the less the time period(T). The following animation shows it explicitly:

 

Interactive Spring - with Different Spring Constants

 

 

 

Finding a good text book - without space-devouring silly cartoons - for physics can be as challenging as mastering the subject.
So,Vivax Solutions highly recommends the following books for you to complement what you learn here:Practice in Physics contains a huge collection of problems for practising; A-Level physics is a great text book to get an in-depth understanding of every major topic in physics.

Graphs of Simple Harmonic Motion: SHM Graphs

Let x = A cos(ωt) where x, ω and t are the displacement, angular velocity and time respectively.
So, velocity = dx/dt = -Aω sin(ωt)
v = -Aω sin(ωt)
acceleration = d²x/dt² = -Aω² cos(ωt)
a = -Aω² cos(ωt)
x = A cos(ωt) | v = -Aω sin(ωt) | a = -Aω² cos(ωt)

The three graphs are as follows; you can practise them interactively; please move the slider, to change the time.

Elastic Potential Energy Stored in a Spring

Suppose a spring with spring constant(k) is stretched by dx. If the work done is dw,
dw = F.dx, where F is the force
So, the total work done, W = ₀ ^x ∫f dx
W = ₀ ^x ∫kx dx
W = 1/2 kx²
The work done is stored in the spring as elastic potential energy.

E = 1/2 kx²

Total Energy involved in SHM

 

For an object attached to a spring,
Potential Energy = 1/2 * k *x² = 1/2 * k* A² sin²(ωt) - as proven above
Kinetic Energy = 1/2 m * A²ω² cos²(ωt)
Total Energy = Potential Energy + Kinetic Energy
= 1/2 * k* A² sin²(ωt) + 1/2 m * A²ω² cos²(ωt)
For the oscillation of the spring, however, ω² = k/m
Substituting this in the above,
Total Energy = 1/2 * k* A² sin²(ωt) + 1/2 m * A²* k/m cos²(ωt)
= 1/2 * k* A² sin²(ωt) + 1/2 * A²*k cos²(ωt)
= [1/2 * k* A²][sin²(ωt) + cos²(ωt)]
= [1/2 * k* A²] * 1 = [1/2 * k* A²] = k' = constant.
Therefore, total energy of the system remains constant.
That means, if the potential energy goes down, the kinetic energy goes up or vice versa.

The following animation sums it up:

 

 

 

Combined Springs - in parallel and series

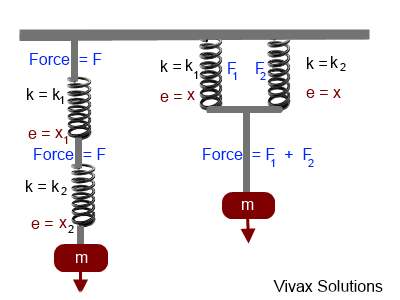
Springs in Series

Total extension = x₁ + x₂
Since F = Ke => e = F/k
Total extension = F/k₁ + F/k₂
= F(1/k₁ + 1/k₂)
If the two springs can be substituted with a single spring of spring constant, k_E,
Total extension = F/k_E
F/k_E = F(1/k₁ + 1/k₂)
1/k_E = 1/k₁ + 1/k₂

1/k_E = 1/k₁ + 1/k₂

Springs in Parallel

Total force = F₁ + F₂
Since F = Ke
Total force = F₁ + F₂
= k₁x + k₂x
If the two springs can be substituted with a single spring of spring constant, k_E,
Total force = k_Ex
k_E = k₁ + k₂

k_E = k₁ + k₂

Damping

The amplitude of the vibration of any object that undergoes SHM, in practice, goes down with time. This is due the inevitable energy losses suffered by the object, being subjected to friction exerted by air particles. This phenomenon is called damping.

Damping can be light, hard or critical, depending on the speed of the loss of amplitude.The following animation illustrates damping. Please stop the animation, before choosing the damping level; then, start again.

 

 

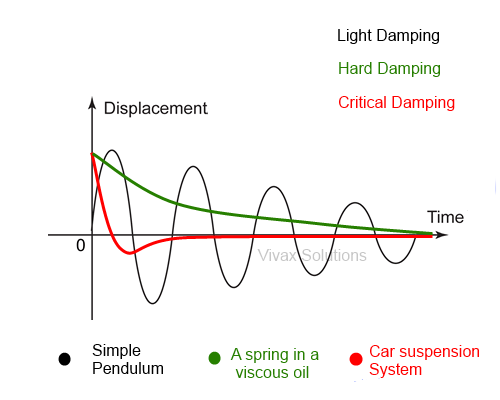
1) Light Damping

E.g. Simple Pendulum

The amplitude of the oscillation slowly goes down with the period of oscillation remaining the same. It means, period of oscillation is independent of the amplitude. This happens due to friction between the pendulum and the air that surrounds it.

2) Hard Damping

E.g. A spring inside a highly viscous oil

The amplitude of the spring goes down without further oscillation and then become stationary.

3) Critical Damping

E.g. Car suspension system

The amplitude rapidly goes down, then without shooting up, it become stationary. This is really important for a car as passengers do not want to experience a discomfort, if the vehicle start oscillation in the event of going over a hump.

Please work out the following questions to complement what you have just learnt.

1. When a pendulum swings, the velocity at the highest point is zero, when the acceleration is maximum. Explain.
2. Discuss the assumptions made in deriving the equation of SHM of the objects attached to springs.
3. A ball bearing is released from rest on the surface of a concave mirror. The diameter of the mirror is small. Show the motion of the ball bearing is SHM and hence derive an expression for its time period.
4. A mass of 0.4kg is attached to a spring of spring constant 10.0 N/m. If the mass undergoes SHM, what will be its frequency?
5. The mass of an object is 30g and is attached to a vertical spring, which stretches 10.0 cm. It is then stretched an additional 5cm and released. Find its period of motion.
6. An SHM has a frequency of 5Hz and an amplitude of 8cm. What is the maximum acceleration? What is the acceleration when t = 0.12 s?
7. A 20g mass is attached to a spring of spring constant 6.0 N/m. The spring is stretched by 8cm and then released. Find the displacement, velocity, and acceleration of the mass when the time is 0.2s.
8. A 14b mass is attached to a vertical spring and it stretches 12cm. It is then stretched by further 4cm and then released. What are the maximum velocity of the mass and its maximum acceleration in these circumstances?
9. A mass of 2kg is placed on a vertical spring attached to a bench and the spring compresses by 15cm. It is then pushed down an additional 8cm and then released. Find (a) the spring constant, (b) the angular frequency, (c) the frequency, (d) the period, (e) the maximum velocity of the mass, (f) the maximum acceleration of the mass.
10. 3. An object of mass, 20g, is attached to a horizontal spring on a smooth table. The spring constant is 5N/m. The spring is then stretched 8cm, before being released. Calculate the total energy of the object, stating your assumptions. What is the potential and kinetic energy of the object, when x = 4cm?
11. The time period of a simple pendulum at the Equator and the North Pole are 14s and 14.5 seconds respectively. Assuming g=9.8ms^-2 at the equator, find the corresponding value at the North Pole.
12. A rectangular object is placed on a smooth table. Its ends are then connected to two identical springs, on two opposite sides. The system is then pushed aside and released. Show that it undergoes SHM.