Quadratic Equations - word problems with solutions

In this tutorial, you will learn:

 

In order to learn how to solve quadratic equations by four different methods, please follow this tutorial; it's detailed and offers plenty of worked examples and practice questions.

In this tutorial, I assume you have already got a good skill in solving quadratic equations as explained in the above tutorial. This tutorial primarily focuses on solving real-world problems involving quadratic equations.

If you think you need a bit more practice before dealing with word problems, here is a question generator and a programme to check your answers:

The Equation Generator

The following programme is interactive: by clicking on the buttons, you can generate a random equation and its solutions: they are randomly generated - and unlimited in number.

 

 

 

The Quadratic Solver

A quadratic equation takes the form of ax² + bx + c where a and b are two integers, known as coefficients of x² and x respectively and c, a constant.

Enter a, b and c to find the solutions of the equations.

E.g.

x² - x - 6 = 0, where a = 1; b=-1; c=-6

 

 

Quadratic Word Problems

 

E.g.1

The sum of two numbers is 27 and their product is 50. Find the numbers.
Let one number be x. Then the other number is 50/x.
x + 50/x = 27
X => x x² + 50 = 27x
- 27x => x² - 27x + 50 = 0
(x -25)(x -2) = 0
(x -25) = 0 or (x -2) = 0
x = 25 or x = 2.

E.g.2

The length of a rectangle is 5 cm more than its width and the area is 50cm². Find the length, width and the perimeter.
Let the width be x. Then the length = x + 5.
x(x + 5) = 50
x² + 5x = 50
-50 => x² + 5x - 50 = 0
(x + 10)(x -5) =0
(x + 10) = 0 or (x -5) =0
x = -10 or x = 5 - x = -10 is impossible to be a width
Width = 5cm; so, the length = 10cm.
Perimeter = 30cm.

E.g.3

The three sides of a right-angled triangle are x, x+1 and 5. Find x and the area, if the longest side is 5.
The hypotenuse = 5
x² + (x+1)² = 5² (Pythagoras' Theorem)
x² + x² + 2x + 1 = 25
-25 => x² + x² + 2x - 24 = 0
2x² + 2x - 24 = 0
x² + x - 12 = 0
(x - 3)(x + 4) = 0
(x + 4) = 0 or (x - 3) = 0
x = -4 or x = 3
x = 3;
Area = 1/2 x 3 x 4 = 6cm²

E.g.4

The product of two numbers is 24 and the mean is 5. Find the numbers.
Let one number = x; then the other = 24/x
(x + 24/x)/2 = 5
X 2 => x + 24/x = 10
X x => x² + 24 = 10x
- 10x => x² + -10x + 24 = 0
(x - 6)(x -4) = 0
(x - 6) = 0 or (x -4) = 0
x = 6 or x =4
The numbers are 6 or 4.

E.g.5

The sum of numbers is 9. The squares of the numbers is 41. Find the numbers.
These are quadratic simultaneous equations.
let the numbers be x and y.
x + y = 9
x² + y² = 41
From the first equation, y = (9-x)
Now substitute this in the second equation.
x² + (9-x)² = 41
x² + 81 - 18x + x² = 41
2x² - 16x + 81 = 41
2x² - 16x + 40 = 0
x² - 8x + 20 = 0
(x - 5)(x -4) =0
(x - 5) = 0 or (x -4) =0
x = 5 or x = 4
Substitute in the first equation, y = 5 or 4
The numbers are 5 and 4.

 

Mathematical Modelling with Quadratic Functions

There are quite a few real life situations that can be modelled by a quadratic function in an accurate way. For instance, the motion of a ball, thrown upwards to move under gravity, can be easily modelled by a quadratic equation. Using the model, we can calculate the height of the ball if the time is known or vice versa.

 

E.g.6

A ball is thrown upwards from a rooftop, 80m above the ground. It will reach a maximum vertical height and then fall back to the ground. The height of the ball from the ground at time t is h, which is given by,
h = -16t² + 64t + 80.

1. What is the height reached by the ball after 1 second?
2. What is the maximum height reached by the ball?
3. How long will it take before hitting the ground?

Follow the graph along with the calculation for a better understanding:

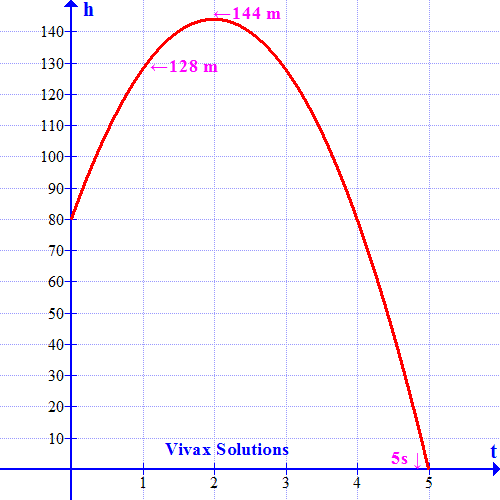
1) h = -16t² + 64t + 80
h = -16* 1*1 + 64*1 + 80 = 128m
2) Rearrange by the completing the square, we get:
h = -16[t² - 4t - 5]
h = -16[(t - 2)² - 9]
h = -16(t - 2)² + 144
When the height is maximum, t = 2; therefore, maximum height = 144m.
3) When the ball hits the ground, h = 0;
-16t² + 64t + 80 = 0
Divide the equation by -16
t² - 4t - 5 = 0
(t - 5)(t + 1) = 0
t = 5 or t = -1
The time cannot be negative; so, the time = 5 seconds.

 

 

E.g.7

A farmer wants to make a rectangular pen for his sheep. He has 60m fencing material to cover three sides with the other side being a brick wall. How should he use the fencing material to maximize the space for his sheep? How should he choose length and width of the pen to achieve his objective?

 

He just has to cover three sides; let the width be x.
Then the length = (60-2x)
Area of the pen = x(60-2x)
= 60x -2x²
Now let's sketch a graph for the quadratic equation. Which is as follows:

 

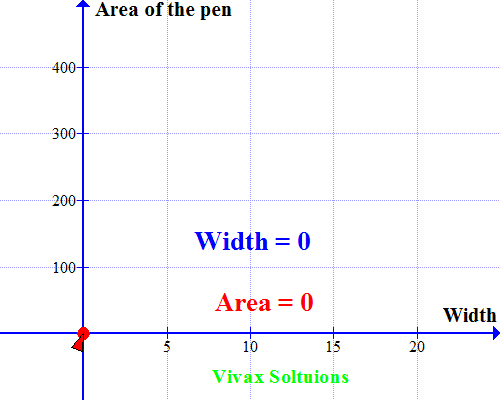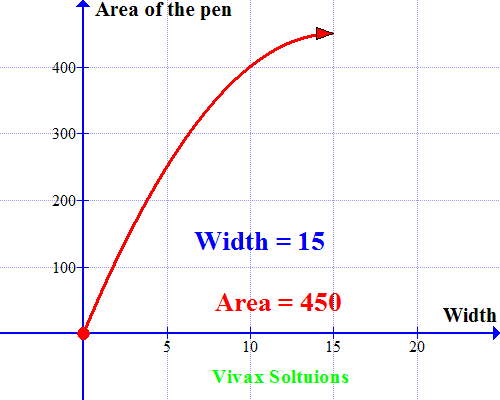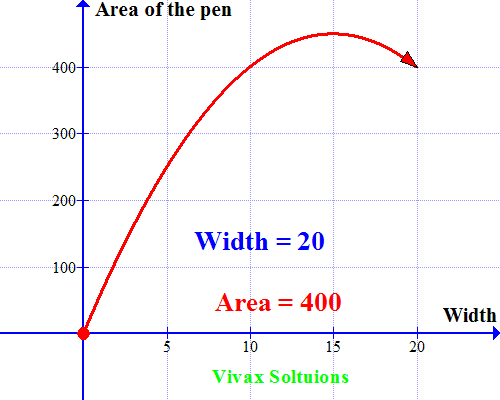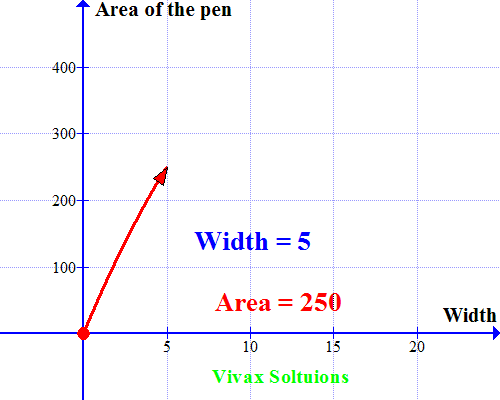
As you can see, the curve peaks at x = 15; when the width = 15m, the area is maximum. A very useful way to use quadratic equations in real life, indeed!

 

E.g.8

Two resistors, when connected in series, have a total resistance of 25 Ohms. If they are connected in parallel, the value goes down to 6 Ohms. Find the values.

When they are in series, if one resistor is x, then the other is 25-x
When they are in parallel, 1/6 = 1/x + 1/(25-x)
1/6 = 25/[x(25-x)] = 25/[25x - x²]
25x - x² = 150
If ax² + bx + c = 0, then
x = [-b ±√(b² - 4ac) ]/ 2a
x² - 25x + 150 = 0
a = 1; b = -25; c = 150
x = -(-25) ±√((-25)² - 4(1)(150)) / 2(1)
x = 25 ±√(625 - 600) / 2
x = 25 ±√(25) / 2
x = (25 ± 5 )/ 2
x = 15 or x = 10
So, the resistors are 15 Ohms or 10 Ohms.

 

E.g.9

The following picture shows the shape of a certain grass patch. If the area of the patch is 80m², find k.

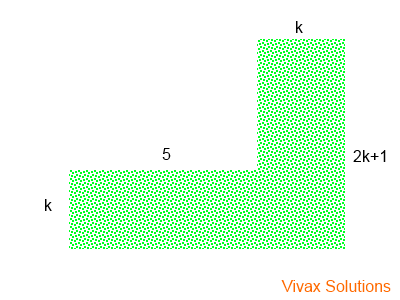
The total area = 5k + k(2k+1)
= 5k + 2k² + k
= 2k² + 6k
Since the area is 80m²
2k² + 6k = 80
2k² + 6k - 80 = 0
(2k - 10)(k + 8) = 0
k = 5 or k = -8
Since the length cannot be negative, k = 5.

 

E.g.10

The following picture shows the shape of a rectangle from which a smaller rectangular part is removed. If the remaining area of the larger rectangle is 35cm², find k.

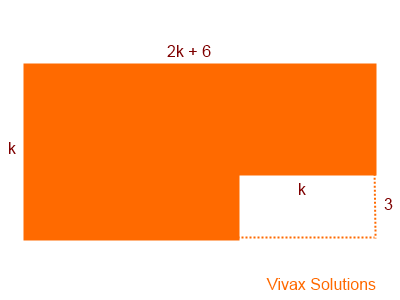
The remaining area = k(2k+6) - 3k
= 2k² + 6k -3k
= 2k² + 3k
Since the area is 35cm²
2k² + 3k = 35
2k² + 3k - 35 = 0
(2k -7)(k + 5) = 0
k = 3.5 or k = -5
Since the length cannot be negative, k = 3.5.

 

E.g.11

The shortest side of a right-angled triangle is 6cm shorter than its hypotenuse. The difference in length of other two sides is 3cm. If the shortest side is n-3, show that 2n² = 12n. Hence, find n.

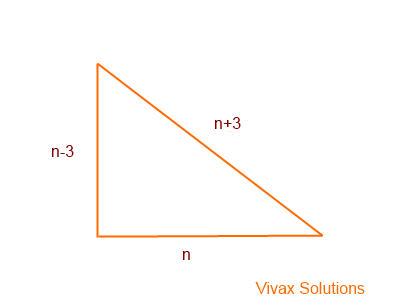
If the length of the shortest side is n-3, the length of the hypotenuse and the other side are n+3 and n respectively.
So, using Pythagoras Theorem,
(n-3)² + n² = (n+3)²
n² - 6n + 9 + n² = n² + 6n + 9
n² = 12n
n² - 12n = 0
n(n - 12) = 0
n = 0 or n = 12.
Since the length cannot be zero, n = 12.

 

E.g.12

Two cyclists move away from a town along two perpendicular paths at 20 mph and 40 mph respectively. The second cyclist starts the journey an hour later than the first one. Find the time taken for them to be 100 miles apart.

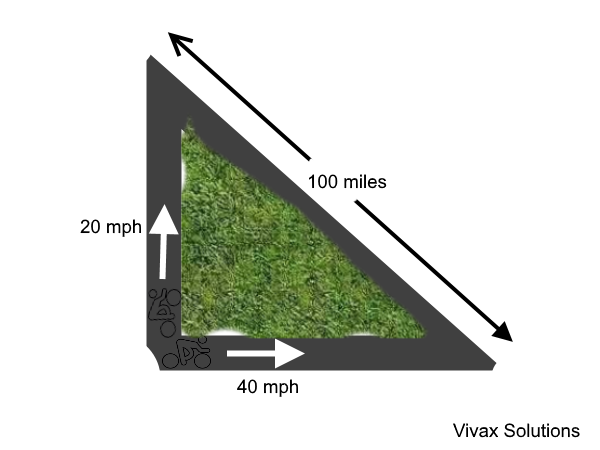
Suppose the time taken by the first cyclist is t; then the time taken by the other cyclist = (t-1)
The distances travelled by them are 20t and 40(t-1) respectively.
Using Pythagoras Theorem,
(20t)² + [40(t-1)]² = 100²
400t² + 1600(t-1)² = 10000
t² + 4t² - 8t + 4 = 25
5t² - 8t -21 = 0
(5t + 7)(t -3) = 0
t = 3 or t = -1.4
Since time cannot be negative, t = 3hrs.

 

 

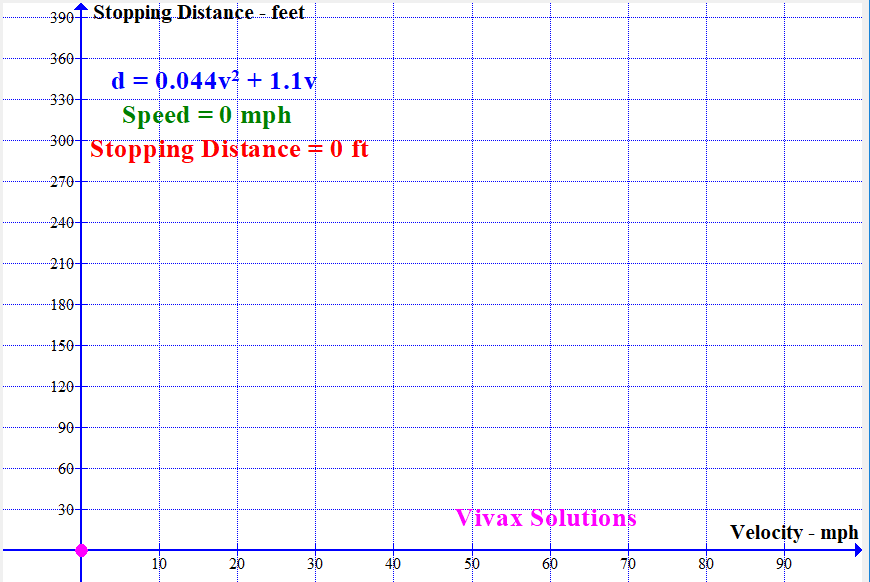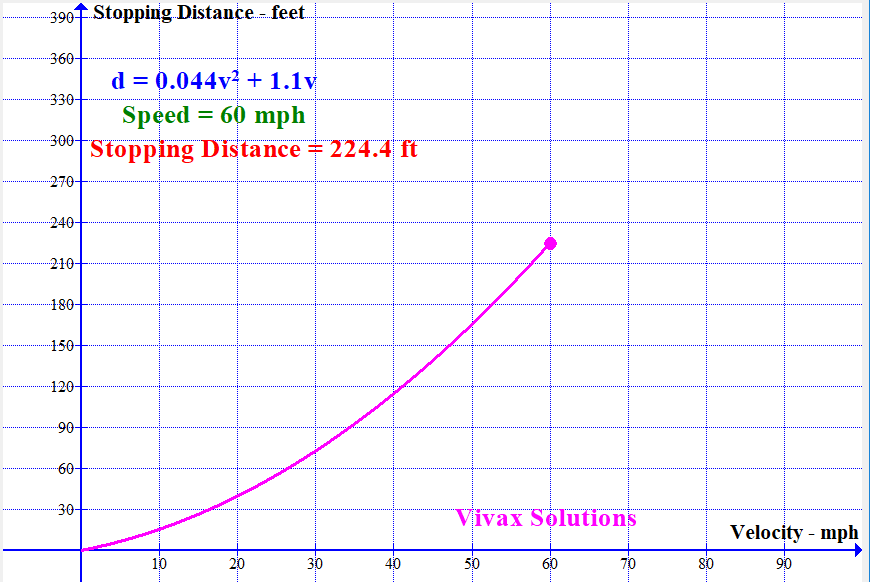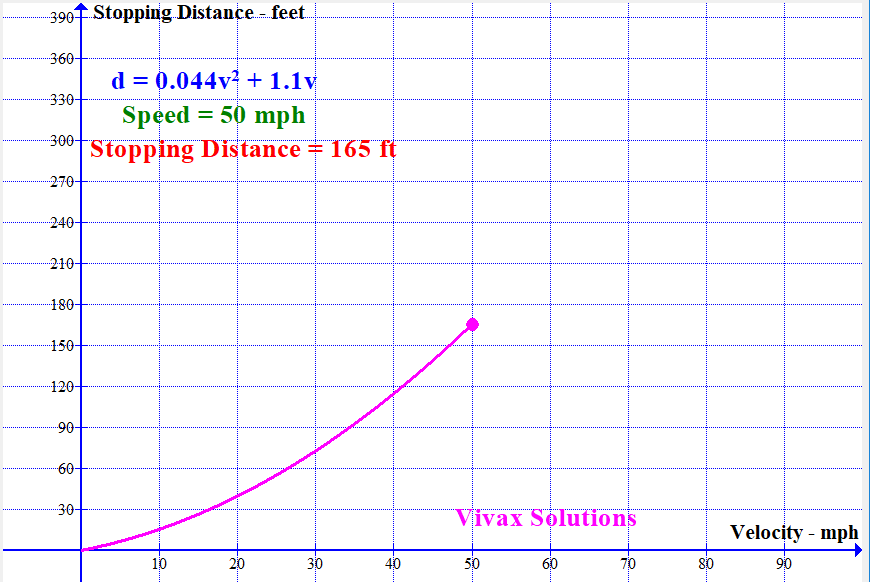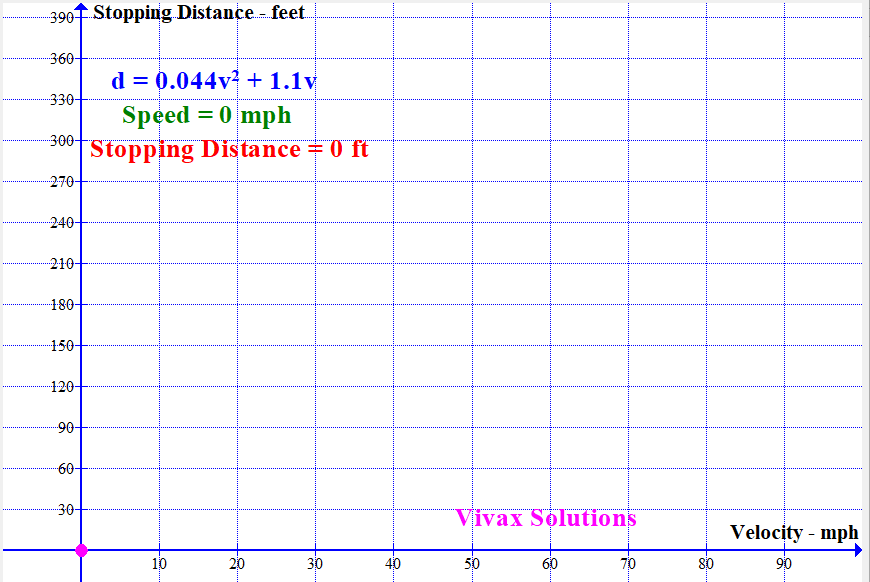
Modelling Stopping Distance of a Vehicle with Speed

With the available data, the stopping distance - sum of thinking distance and breaking distance - can be modelled by a quadratic function. It is as follows:

 

Stopping Distance
Thinking Distance	Breaking Distance

 

If the stopping distance = d and the speed = v,
d = 0.044v² + 1.1v

The following animation shows how the stopping distance, modelled by the above equation, changes with the speed:

 

 

Infinite Square Root Problem

Solve the following infinite square root problem:

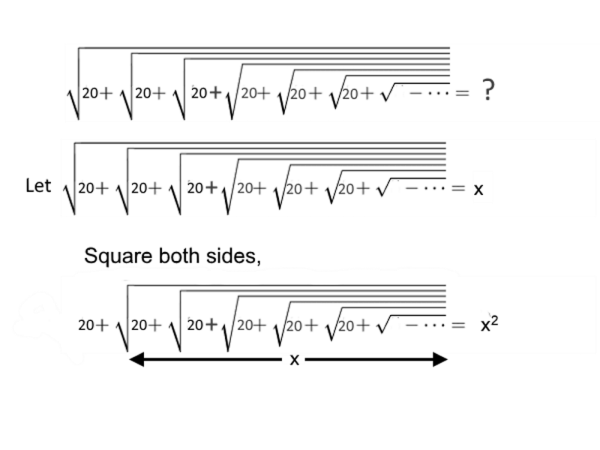
20 + x = x²
x² - x - 20 = 0
x = (1 ± √1 + 80)/2
x = (1 ± √81)/2
x = (1 ± 9)/2
x = 5 or x = -4
Since the square root of a negative number cannot be found, x = 5. So, the value of the above infinite square problem is 5.

 

🏆 Challenging Questions

 

1) Solve the following equation and find all the possible values of x:

(x² - x - 5)^{x² - 2x - 3} = 1

2) Show that x² -2xy + 2y² can never be a negative.

 

Ad: The author of this site offers fully interactive tutorial on differentiation

 

Now, in order to complement what you have just learnt, work out the following questions:

Questions

1. The sum of squares of two consecutive even numbers is 244. Find the numbers.
2. The base length of a triangle is 2cm more than its height. The area is 24cm². Find the length of hypotenuse and the perimeter of the triangle.
3. The length of a square is increased by a 5^th so that its new area is 44cm² more than the original value. Find the difference in perimeter of two shapes.
4. The length and width of a rectangular garden are 150m and 120m. A foot path of regular width is added to the boundary of the garden and the total area of the garden becomes 2800m² more than its original area. Find the width of the footpath.
5. Adam is about to embark on a journey on a narrow country lane that covers 32km and decides to go at x km/h. On second thoughts, he calculates that if he increases the speed by 4km/h, his journey time can be cut down by 4 hrs. Find x.
6. The reciprocal of the sum of reciprocals of two numbers is 6. The sum of numbers is 25. Find the numbers.
7. The speed of an ant is (2t + 10) and after travelling for t minutes, it covers a distance of 12m. Find t.
8. Two chords and a diameter form a triangle inside a circle. The radius is 5cm and one chord is 2cm longer than the other one. Find the perimeter and the area of the triangle.
9. The sum of a number and it reciprocal is 26/5. Find the number.
10. The product of two numbers is 20. The sum of squares is 41. Find the numbers.
11. The dimensions of the glass plate of a wedding photo are 18cm and 12cm respectively. A new rectangular frame of equal width all, the way round the photo, is about to be fitted around the it so that the area of the frame is the same as that of the glass. Find the width of the frame.
12. A group of acquaints went to a restaurants for a meal. When the bill for £175 was brought by a waiter, two of the cheeky ones from the group just sneaked off before the bill was paid, which resulted in the payment of extra £10 by each remaining individual. How many were in the group at first?
13. Ashwin and Donald decided to set out from two towns on their bikes, which are 247 miles apart, connected by a straight t Roman road in England. When they finally met up somewhere between the two towns, Ashwin had been cycling for 9 miles a day. The number of days for the whole adventure is 3 more than the number of miles that Donald had been cycling in a day. How many miles did each cycle?
14. When a two-digit number is divided by the product of the two digits, the answer is 2 and if 27 is added to the number, the original number turns into a new number with the digits being swapped around. Find the number.
15. There are three numbers: the difference of the differences of them is 5. The sum and product are 44 and 1950 respectively. Find the numbers.
16. Find the two numbers, whose sum is 19 and the product of the difference and the greater, is 60.
17. A boy was asked his age: "If you add the square root of it to half of it, and then subtract 12, the answer will be nothing," replied the boy. What was his age?
18. A group of army cadets, consisting of 1066 men, form two squares in front of a garrison. In the side of one square, there are 4 more men than the other. How many men are in each side of the squares?
19. The height of a triangle is 4cm less than three times its base length. If the area is 80 cm², find the lengths of the base and height.
20. An isosceles triangle is inscribed in a circle in such a way that its longest side, which goes through the centre is √50cm. Find the area of the triangle.
21. A butcher bought some pheasants for £100.00. Had each cost £1 less, he would have bought 5 more. How many pheasants did he buy?
22. The sum of reciprocals of two consecutive integers is 13/42. Find the integers.
23. The product of two numbers and the difference between them are 289 and 20 respectively. Find the numbers.
24. The sum of two numbers is 20. The sum of squares is 250. Find the numbers.
25. The area of a square exceeds twice that of another by 56cm². If the difference of the perimeter between the two is 24cm, find the area of the smaller square.

 

Answers

Move the mouse over, just below this, to see the answers:

1. 10, 12
2. 10cm, 24cm
3. 8cm
4. 5m
5. 4km/h
6. 10, 15
7. 1
8. 24cm, 24cm²
9. 5
10. 5 and 4
11. 3cm
12. 7
13. 117 and 130 miles
14. 36
15. 6, 13, 25
16. 12,7
17. 16
18. 21 and 25
19. 8cm, 20cm
20. 12.5cm²
21. 20
22. 6, 7
23. 27, 7
24. 15, 5
25. 100 or 4

 

Do you need detailed solutions to the above questions? Please click the following and I will send the answers:

Detailed Solutions
for the above
Quadratic Questions
As a PDF
for Just £3.99

 

Now that you have read this tutorial, you will find the following tutorials very helpful too: