Kinematics - Equations of Motion

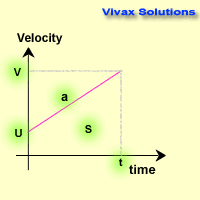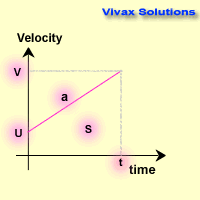
Suppose an object starts moving at u and gains an acceleration of a. After time t, it gets a speed v after travelling a distance of s. The graph shows this data on a velocity-time grid.

a = (v - u) / t => v - u = at

v = u + at

s = ut + 1/2(v - u) t
s = ut + 1/2 (at) t
s = ut + 1/2 at²

s = ut + 1/2 at²

v² = (u + at)²
v² =u² + 2uat + a²t²
v² = u² + 2a (ut + 1/2 at²)
v² = u² + 2as

v² = u² + 2as

 

You can learn the relationship between the displacement-time, velocity-time and acceleration-time graphs with the following interactive applet. Just move the slider - the time - and see the corresponding change in displacement, velocity and acceleration.

 

 

 

E.g.1

An object starts from rest and moves with an acceleration 2 ms^-2. Find its speed after 5 seconds and distance travelled.
u = 0, t = 5s, a = 2
v = 0 + 2 x 5
v = 10 ms^-1
s = ut + 1/2 at²
s = 0 + 1/2 x 2 x 25
s = 25m.

E.g.2

An object starts moving at 10 ms^-1 and gains an acceleration of 2 ms^-2. Find its speed after 5 seconds and the distance travelled.
u = 10, a = 2, t = 5
v = 10 + 2 x 5
v = 20 ms^-1 s = ut + 1/2 at²
s = 10x5 + 1/2 x 2 x 25
s = 75m.

E.g.3

An object start moving at 20 ms^-1 and increases its speed to 40ms^-1 in 5 seconds. Find its acceleration and the distance travelled during this time.
v = 40, u = 20, t = 5
40 = 20 + 5a
5a = 20
a = 4 ms^-2
s = 20 x 5 + 1/2 x 4 x 25
s = 100 + 50
s = 150 m

E.g.4

An object starts moving at 20ms^-1 and reduces speed to 10 ms^-1 in 2 seconds. Find its deceleration and the distance travelled. How far further will it move before coming to a halt?
u = 20, v = 10, t = 2,
10 = 20 + 2a
2a = -10
a = -5 ms^-2
s = 20 x 2 - 1/2 x 5 x 4
s = 40 - 10
s = 30 m
When it stops,
v = 0, u = 10, a = -5
0 = 100 + 2 x -5 x s
10s = 100
s = 10 m

E.g.5

An object start moving at 10 ms^-1 with an acceleration 2ms^-2. Calculated the distance travelled by it during the third second.
u = 10, a = 2, t = 2
s = 10 x 2 + 1/2 x 2 x 4
s = 20 + 4
s = 24 m
u = 10, a = 2, t = 3
s = 10 x 3 + 1/2 x 2 x 9
s = 30 + 9
s = 39 m
Distance travelled during the third second = 39 - 24 = 15m.

E.g.6

A ball is thrown upwards at 20 ms^-1. Find the time taken by it before reaching a height of 15 m. Assume g = 10 ms^-2. Hence account for the answers.
u = 20, a = -10 s = 15
15 = 20t - 1/2 x 10 x t²
5t² - 20t + 15 = 0
t² - 4t + 3 = 0
(t - 3)(t-1) = 0
t = 3 or t = 1
There are two possible values for the time - both acceptable on account of being positive;
The object can be at the height of 15m on two occasions - while going up and coming down.

 

E.g.7

The height of a tower is 20m. A ball is thrown up at 20 m/s from the tower. How long will the ball take to hit the ground? Assume g=10ms^-2.
In this case, when the ball hits the ground, the displacement is -20m.
s = -20, u = 20 a = -10 t = ?
s = ut + 1/2 at²
-20 = 20*t - 1/2 10 x t²
-20 = 20t - 5t²
t² -4t -4 = 0
t = 4.8s or t = -0.83s
Since time cannot be negative, t=4.8s.

E.g.8

A balloon has been ascending at a constant speed of 20m/s. When it reaches a height, 40m, an iron nails falls off the balloon. How long will it take before the nail hits the ground, assuming g=10ms^-2.? What are the assumptions that you make?
Since the balloon has been ascending at 20m/s, when the nail was dropped, the speed of the nail is also 20m/s. Afterwards, the nail moves under gravity, upwards until it stops and then falls back again.
So, the displacement of the nail with respect to the ground is -40m.
s = -40, u = 40 a = -10 t = ?
s = ut + 1/2 at²
-40 = 20*t - 1/2 10 x t²
-40 = 20t - 5t²
t² -4t -8 = 0
t = 5.46s or t = -1.46s
Since time cannot be negative, t= 5.46s.
Air resistance is ignored during the calculations.

E.g.9

A car is moving at a constant acceleration, passing three towns A, B, C along the way. The distance between A and C is 200 km. It passes the three towns at t = 0, t = 4 and t = 10 seconds respectively. If the velocity of the car when it passes town A is 10km/s, find the acceleration and the distance BC.
A--->B
u = 10, a = ? t = 4, s = ?
s = 10 x 4 + 1/2 x a x 16
s = 40 + 8a 1
A--->C
u = 10, a = ? t = 10, s = 200
200 = 10 x 10 + 1/2 x a x 100
50a = 100
a = 2ms^-2
Sub in 1
s = 40 + 8x 2
s = 56km.
So, distance between B and C is 200 - 56 = 144km.

E.g.10

A man runs past three poles, P, Q and R, at 20m/s, 12m/s and 8m/s respectively. Show that PQ:QR = 16: 5.
P--->Q
s = s_PQ u = 20 v = 12
v² = u² + 2as
144 = 400 + 2as_PQ
-256 = 2as_pq 1
Q--->R
s = s_QR u = 12 v = 8
v² = u² + 2as
64 = 144 + 2as_QR
-80 = 2as_PQ 2
1 / 2
s_PQ / s_QR = 144/80 = 16/5
s_PQ : s_QR = 16 : 5

E.g.11

An ant is moving with a constant acceleration. It has been observed that it travels a distance of 720mm and 960mm respectively during the eleventh and fifteenth seconds respectively. Find the initial velocity and the acceleration. Hence find the distance travelled by the ant after 20 seconds as well.
0---1---2----------------------------10-720mm-11----------------14-960mm-15------20<
Let the initial velocity and acceleration be v and a respectively.
s = ut + 1/2 at²
So, s₁₀ = 10u + 1/2 a* 100 = 10u + 50a 1
s₁₁ = 11u + 1/2 a* 121 = 10u + 60.5a 2
2 - 1 => 720 = u + 10.5a 3
In the same way,
So, s₁₄ = 14u + 1/2 a* 196 = 14u + 98a 4
s₁₅ = 15u + 1/2 a* 225 = 14u + 112.5a 5
5 - 4 => 960 = u + 14.5a 6
6 - 3 => 240 = 4a => a = 60 mm/s².
Sub in 3 => 720 = u + 10.5 x 60
u = 90 mm/s.
s₂₀ = 20x90 + 1/2x60x 400 = 1800 + 12000 = 13800mm.

E.g.12

Assuming that the acceleration due to gravity on the Earth is 9.6 ms^-2, find the height reached by an object, projected vertically upwards on the Moon at 16 m/s. The gravity on the Moon is 1/6 ^th of that on the Earth.
v² = u² + 2as
0 = 256 - 2 x 1.6 x s
s = 80m.

 

 

Ad:The author's fully interactive tutorial on differentiation

 

Motion with varying acceleration

As you have already seen, in every single above example, the object/s in question was/were moving at a constant acceleration. If the acceleration changes, the equations of motion become just redundant. So, we have to use differentiation in order to deal with problems involving varying acceleration.

E.g.1

The displacement of an object varies with time as t³/3 - 2t² + 3t.

1. Find its velocity and acceleration in terms of t.
2. Find the initial velocity.
3. Find the velocity when t = 2.
4. Find the acceleration when t = 4.
5. When does it change the direction of its velocity?
6. When does it have zero acceleration?

 

1. v = ds/dt = t² -4t + 3
   t = 0 => v = 3 m/s
2. s = t³/3 - 2t² + 3t
   v = ds/dt = t² -4t + 3
   a = dv/dt = 2t -4
3. v = t² -4t + 3
   t = 2 => v = -1 m/s
4. a = dv/dt = 2t -4
   t = 4 => a = 4 ms^-2
5. It changes velocity when t = 1 and t = 3 - velocity changes from positive to negative and vice versa.
6. a = 2t - 4
   a = 0 => t = 2s.

E.g.2

An object moves along the x-axis at a velocity, v = 12t + t²/3. The distance from the origin, O, when time = t is x. Find its acceleration, when t = 3s. If x = -10, when t = 0, derive an expression for the displacement. Hence find the displacement when t = 4s.

1. a = dv/dt = 12 + 2t/3
   t = 3 => a = 14 ms^-2
2. s = ∫v dt
   = 12t²/2 + t³/9 + c
   = 6t² + t³/9 + c
   t = 0, s = -10;
   -10 = c
   s = 6t² + t³/9 - 10
   t = 4 => s = 96 + 64/9 - 10
   s = 93.1 m.

 

---

Recommended Book for new A Level Maths

This is good workbook for both teachers and students alike: teachers can set homework from this book; students can learn from the worked examples that are well-structured. Since maths revision is practice-centred, this book offers a good resource with plenty of questions for that purpose.

 

 

 

---

---

Questions for Practice

Please work out the following questions to complement what you have just learnt.

1. The speed of a car goes down from 40 ms^-1 to 35 ms^-1 in 1/2 seconds. Find its deceleration. How far will it move further before stopping?
2. A car starts from rest and moves with an acceleration 4ms^-2. Find its speed after 6 seconds and the distance travelled during that time.
3. A stone is dropped into a well. Its splash could be heard after 4.25 seconds since its drop. Calculate the depth of the well, if the speed of sound is 320 ms^-1 and g = 10 ms^-2.
4. A stone is dropped from the top of a tower. It goes through 16/25^th of the total height during the last second. Find the height of the tower and the time taken for the fall. g = 10ms^-2
5. A balloon is ascending at a constant speed of 20 ms^-1. An object falls from it after 4 s in motion. Find the distance travelled by the object before it hits the ground. g = 10 ms^-2.
6. A vehicle is moving at a constant acceleration. It passes the town P at 66 kmh^-1 and town Q at 74kmh^-1, a distance of 40 km between the two. Find the acceleration. Hence, find the time taken by the vehicle to move past the first kilometre post, after passing P.
7. A car accelerates at 4ms^-2, starting from rest, for 5 seconds, then maintains the speed for 10 seconds, and eventually slows down to a halt in 4 seconds. Find the deceleration during the final stage and the total distance covered. What is the average speed of the car?
8. A car starts from rest and moves with an acceleration of 4ms^-2 for 20 seconds. It then comes to a halt in the next 5 seconds. Find the deceleration of the car and the distance covered during the first 22 seconds.
9. A car has been moving at a constant speed of 20ms^-1. A lorry starting from rest moves with an acceleration of 4ms^-2. How long will the lorry take before it gets the same speed of the car? How far have both gone by then? Find the time taken by the lorry to catch with the car and the distance travelled by then as well.
10. An object slows down its speed from 20ms^-1 to 10ms^-1 in 4 seconds. Find its deceleration and the distanced travelled. It then comes to a halt in 5 seconds at a different deceleration. Find the total distance travelled by the object.
11. A bucket is lowered into a well at a constant acceleration of 2 ms^-2. After 10 seconds, a ball is dropped into the bucket from rest, while the latter was still in motion. How long will the ball take to fall into the bucket?
12. A stone is projected vertically at a speed, which is just enough for it to reach a height, 90m. Two seconds later, a second stone is projected upwards in the same way. When will the two stones meet up? Find the position at which they meet up too. Assume g = 9.6 ms^-2.

 

Answers

Move the mouse over, just below this, to see the answers:

1. -10, 61.25
2. -24, 72
3. 80
4. 125,5
5. 120, 6.47
6. 14, 0.02
7. 5, 190, 13.6
8. 16, 952
9. 5, 100, 50, 10, 200
10. 2.5, 120, 145
11. 3.3
12. 3.5, 25.2

 

Now that you have read this tutorial, you will find the following tutorials very helpful too: